Kết quả tìm kiếm cho: ty so

Đề: Xác định $m$ để đồ thị hàm số $(C):y=x^{4}+4mx^{3}-2x^{2}-12mx$ có trục đối xứng song song với $Oy$.

Ngày 11/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Tâm đối xứng - trục đối xứng

Đề bài: Xác định $m$ để đồ thị hàm số $(C):y=x^{4}+4mx^{3}-2x^{2}-12mx$ có trục đối xứng song song với $Oy$. Lời giải Giả sử đồ thị có trục đối xứng song song với $Oy$ là $x=a(a\neq 0)$Khi đó,với phép biến đổi tọa độ:$\begin{cases} X=x-a \\Y=y\end{cases} \Leftrightarrow \begin{cases} x=X+a \\y=Y \end{cases} $Hàm số $Y=(X+a)^{4}+4m(X+a)^{3}-2(X+a)^{2}-12m(X+a)$ là hàm số … [Đọc thêm...] vềĐề: Xác định $m$ để đồ thị hàm số $(C):y=x^{4}+4mx^{3}-2x^{2}-12mx$ có trục đối xứng song song với $Oy$.

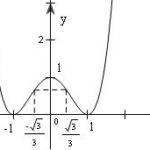
Đề: $1$. Giải phương trình: $x^4 – 2x^2 + 1 = 0$$2$. Khảo sát hàm số: $y = x^4 – 2x^2 + 1$$3$. Biện luận theo $m$ số nghiệm của phương trình: $x^4 – 2x^2 + 1- m = 0$

Ngày 11/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: $1$. Giải phương trình: $x^4 - 2x^2 + 1 = 0$$2$. Khảo sát hàm số: $y = x^4 - 2x^2 + 1$$3$. Biện luận theo $m$ số nghiệm của phương trình: $x^4 - 2x^2 + 1- m = 0$ Lời giải $1.$ Ta có $x^4-2x^2+1=(x^2-1)^2=0\Leftrightarrow x=\pm1$$2.$ Khảo sát hàm số: xin dành cho bạn đọc, đồ thị hàm số như hình vẽ:$3.$ Nghiệm phương trình là hoành độ giao diểm của hai … [Đọc thêm...] vềĐề: $1$. Giải phương trình: $x^4 – 2x^2 + 1 = 0$$2$. Khảo sát hàm số: $y = x^4 – 2x^2 + 1$$3$. Biện luận theo $m$ số nghiệm của phương trình: $x^4 – 2x^2 + 1- m = 0$

Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y = {5^{x – 1}} + {5^{ – x – 1}}$

Ngày 11/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Ứng dụng hàm số vào giải toán

Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y = {5^{x - 1}} + {5^{ - x - 1}}$ Lời giải GiảiTa có:${y^ / } = \left( {{5^{x - 1}} - {5^{ - x - 1}}} \right)\ln 5$ Bảng biến thiên : Vậy : Không có giá trị lớn nhất., khi $x = 0$ … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số: $y = {5^{x – 1}} + {5^{ – x – 1}}$

Đề: Cho ba số dương $a,b,c$ (cho trước) và ba số dương bất kỳ $x,y,z$ luôn luôn thỏa mãn $\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=1$Tìm giá trị nhỏ nhất của biểu thức $P=x+y+z$

Ngày 11/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Giá trị lớn nhất - nhỏ nhất

Đề bài: Cho ba số dương $a,b,c$ (cho trước) và ba số dương bất kỳ $x,y,z$ luôn luôn thỏa mãn $\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=1$Tìm giá trị nhỏ nhất của biểu thức $P=x+y+z$ Lời giải Trong không gian tọa độ $Oxy$ chọn:$\overrightarrow {u}=(\sqrt{x};\sqrt{y};\sqrt{z}) \Rightarrow |\overrightarrow {u}|=\sqrt{x+y+z}$$\overrightarrow … [Đọc thêm...] vềĐề: Cho ba số dương $a,b,c$ (cho trước) và ba số dương bất kỳ $x,y,z$ luôn luôn thỏa mãn $\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=1$Tìm giá trị nhỏ nhất của biểu thức $P=x+y+z$

Đề: a) Chứng minh rằng hàm số: $y=\sin^2 x-14\sin x\cos x-5\cos^2 x+2\sqrt[3]{33}$ chỉ nhận giá trị dương.b) Xác dịnh $a$ để giá trị nhỏ nhất của hàm số $y=4x^2-4ax+a^2-2a$ trên $[-2;0]$ bằng $2$

Ngày 11/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Giá trị lớn nhất - nhỏ nhất

Đề bài: a) Chứng minh rằng hàm số: $y=\sin^2 x-14\sin x\cos x-5\cos^2 x+2\sqrt[3]{33}$ chỉ nhận giá trị dương.b) Xác dịnh $a$ để giá trị nhỏ nhất của hàm số $y=4x^2-4ax+a^2-2a$ trên $[-2;0]$ bằng $2$ Lời giải a) Ta chứng minh $\min y>0$Ta có: $y=\frac{1-\cos 2x}{2}-7\sin 2x-\frac{5(1+\cos 2x)}{2} +3\sqrt[3]{33}$ $=-7\sin 2x-3\cos … [Đọc thêm...] vềĐề: a) Chứng minh rằng hàm số: $y=\sin^2 x-14\sin x\cos x-5\cos^2 x+2\sqrt[3]{33}$ chỉ nhận giá trị dương.b) Xác dịnh $a$ để giá trị nhỏ nhất của hàm số $y=4x^2-4ax+a^2-2a$ trên $[-2;0]$ bằng $2$

Đề: Tìm giá trị nhỏ nhất vs lớn nhất của hàm số: $y=\frac{2\cos^2x+|\cos x|+1}{|\cos x|+1}$.

Ngày 11/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Giá trị lớn nhất - nhỏ nhất

Đề bài: Tìm giá trị nhỏ nhất vs lớn nhất của hàm số: $y=\frac{2\cos^2x+|\cos x|+1}{|\cos x|+1}$. Lời giải Đặt $|\cos x|=t$ điều kiện $0\leq t\leq 1$.Khi đó, ta xét hàm số $y=\frac{2t^2+t+1}{t+1}$ trên tập $D=[0,1]$Đạo hàm : $y^'=\frac{2t^2+4t}{(t+1)^2}>0, \forall t\in D\Rightarrow $ hàm số đồng biến trên $D$.Vậy ,ta nhận được:-$\min y=y(0)=1$, … [Đọc thêm...] vềĐề: Tìm giá trị nhỏ nhất vs lớn nhất của hàm số: $y=\frac{2\cos^2x+|\cos x|+1}{|\cos x|+1}$.

Đề: Cho hàm: $y = \frac{{{x^2} + x – 3}}{{x + 2}}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ kết quả đó, hãy suy ra cách vẽ đồ thị của hàm số: $y = \frac{{{x^2} + x – 3}}{{\left| {x + 2} \right|}}$3) Tìm các điểm thuộc trục hoành sao cho từ mỗi điểm ấy có thể vẽ được đúng một tiếp tuyến tới đồ thị ở phần 1

Ngày 11/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm: $y = \frac{{{x^2} + x - 3}}{{x + 2}}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ kết quả đó, hãy suy ra cách vẽ đồ thị của hàm số: $y = \frac{{{x^2} + x - 3}}{{\left| {x + 2} \right|}}$3) Tìm các điểm thuộc trục hoành sao cho từ mỗi điểm ấy có thể vẽ được đúng một tiếp tuyến tới đồ thị ở phần 1 Lời giải $1)$ Viết … [Đọc thêm...] vềĐề: Cho hàm: $y = \frac{{{x^2} + x – 3}}{{x + 2}}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ kết quả đó, hãy suy ra cách vẽ đồ thị của hàm số: $y = \frac{{{x^2} + x – 3}}{{\left| {x + 2} \right|}}$3) Tìm các điểm thuộc trục hoành sao cho từ mỗi điểm ấy có thể vẽ được đúng một tiếp tuyến tới đồ thị ở phần 1

Đề: Cho $(C):y = 2x^3 – 3x^2 – 12x -5 $ . Viết phương trình tiếp tuyến biết tiếp tuyến đó song song với đường thẳng $ y = 6x – 4 $.

Ngày 11/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Tiếp tuyến của đồ thị

Đề bài: Cho $(C):y = 2x^3 - 3x^2 - 12x -5 $ . Viết phương trình tiếp tuyến biết tiếp tuyến đó song song với đường thẳng $ y = 6x - 4 $. Lời giải Tiếp tuyến song song với đường thẳng: $ y = 6x - 4 $ có dạng $ \left( d \right):y = 6x + b $ với $ b \ne - 4$ ĐK để $ \left( d \right) $ và $ \left( C \right) $ tiếp xúc là hệ sau có nghiệm: $ \left\{ … [Đọc thêm...] vềĐề: Cho $(C):y = 2x^3 – 3x^2 – 12x -5 $ . Viết phương trình tiếp tuyến biết tiếp tuyến đó song song với đường thẳng $ y = 6x – 4 $.