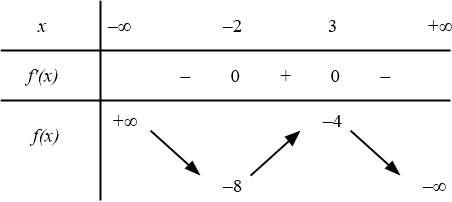
Bài toán gốc Cho hàm số $y=f(x)=ax^3+bx^2+cx+d,a\neq 0$ có đồ thị như hình dưới đây:Chọn phát biểu đúng?A. $a{>}0,d{>}0$.B. $a{<}0,d{<}0$.C. $a{<}0,d{>}0$.D. $a{>}0,d{<}0$. Phân tích và Phương pháp giải Dạng toán nhận biết dấu các hệ số $a, b, c, d$ của hàm đa thức bậc ba $y=ax^3+bx^2+cx+d$ dựa vào đồ thị hàm số.1. Dấu … [Đọc thêm...] vềCho hàm số $y=f(x)=ax^3+bx^2+cx+d,a\neq 0$ có đồ thị như hình dưới đây:
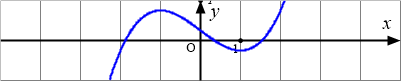
Chọn phát biểu đúng?