Một vật chuyển động, quãng đường $s\left( t \right)$ (tính theo mét) vật đi được sau khoảng thời gian $t$ (tính theo giây), $t\ge 0$

Một vật chuyển động, quãng đường $s\left( t \right)$ (tính theo mét) vật đi được sau khoảng thời gian $t$ (tính theo giây), $t\ge 0$. được mô tả là một hàm số bậc ba có đồ thị như hình vẽ dưới đây:

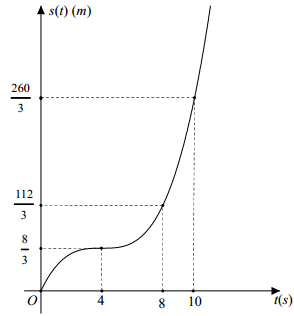
Hỏi trong $10$ giây đầu tiên, khoảng thời gian vật chuyển động nhanh dần kéo dài bao nhiêu giây?

Lời giải

Đáp án: $8$.

Giả sử $s\left( t \right)=a{{t}^{3}}+b{{t}^{2}}+ct+d\left( a\ne 0 \right).$

Vì đồ thị hàm số $s\left( t \right)$ đi qua các điểm $\left( 0;0 \right)$, $\left( 4;\dfrac{8}{3} \right)$, $\left( 8;\dfrac{112}{3} \right)$ và $\left( 10;\dfrac{260}{3} \right)$ nên ta có

$\left\{ \begin{array}{l}

64a+16b+4c=\dfrac{8}{3} \\

512a+64b+8c=\dfrac{112}{3} \\

1000a+100b+10c=\dfrac{260}{3} \\

d=0 \\

\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}

a=\dfrac{1}{6} \\

b=-1 \\

c=2 \\

d=0 \\

\end{array} \right..$

Do đó $s\left( t \right)=\dfrac{1}{6}{{t}^{3}}-{{t}^{2}}+2t.$

Ta có $v\left( t \right)={s}’\left( t \right)=\dfrac{1}{2}{{t}^{2}}-2t+2\Rightarrow$ ${v}’\left( t \right)=t-2=0\Leftrightarrow t=2.$

Bảng biến thiên:

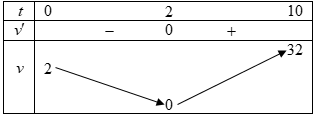
Dựa vào bảng biến thiên, từ giây thứ $2$ trở đi vận tốc của vật tăng dần theo thời gian. Do đó trong $10$ giây đầu tiên, khoảng thời gian vật chuyển động nhanh dần kéo dài trong $8$ giây.