Cho một tấm nhôm hình lục giác đều cạnh $90$ cm

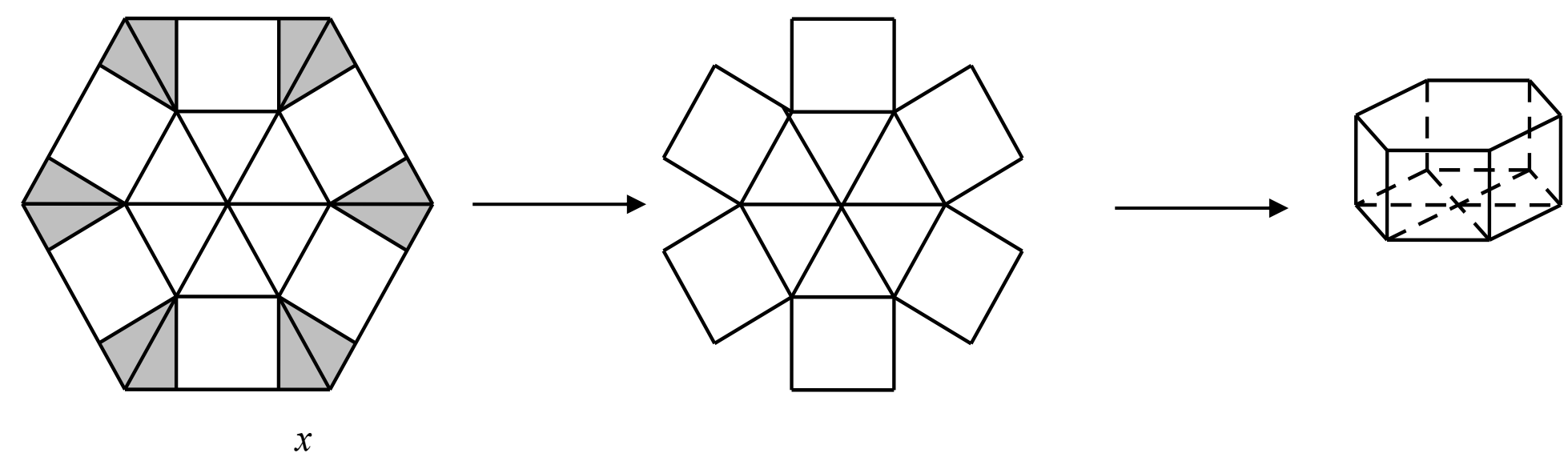
Cho một tấm nhôm hình lục giác đều cạnh $90$ cm. Người ta cắt ở mỗi đỉnh của tấm nhôm hai hình tam giác vuông bằng nhau, biết cạnh góc vuông nhỏ bằng $x$ (cm) (cắt phần tô đậm của tấm nhôm) rồi gập tấm nhôm như hình vẽ để được một hình lăng trụ lục giác đều không có nắp. Tìm $x$ để thể tích của khối lăng trụ lục giác đều trên là lớn nhất (Nếu kết quả là số thập phân thì làm tròn kết quả đến hàng đơn vị).

Lời giải

Đáp án: 15.

Lăng trụ có:

Diện tích đáy:

$\begin{array}{l}

S=6.\dfrac{O{{C}^{2}}\sqrt{3}}{4}=\dfrac{3\sqrt{3}}{2}.{{(OB-BC)}^{2}}=\dfrac{3\sqrt{3}}{2}{{\left( OB-\dfrac{x}{\cos \widehat{ABC}} \right)}^{2}} \\

=\dfrac{3\sqrt{3}}{2}{{\left( 90-2x \right)}^{2}}=6\sqrt{3}{{\left( 45-x \right)}^{2}} \\

\end{array}$

Chiều cao: $h=AC=x.\tan \widehat{ABC}=x\sqrt{3}$

Thể tích lăng trụ: $V=Sh=18x{{(45-x)}^{2}}=18({{x}^{3}}-90{{x}^{2}}+{{45}^{2}})$

Đạo hàm: ${V}’=18(3{{x}^{2}}-180x+{{45}^{2}});{V}’=0\Rightarrow \left[ \begin{array}{l}

x=15\Rightarrow y=243000 \\

x=45\Rightarrow y=0 \\

\end{array} \right.$

x

0

15

45

V’

+

0

−

0

V

0

243000

0

Dựa vào bảng biến thiên ta nhận $x=15.$