Từ năm 2004 đến năm 2019 doanh thu $R\left( t \right)$ (tính bằng triệu đô la) của McDonald’s có thể được mô hình hóa bởi $R\left( t \right)=-130,769{{t}^{3}}+2296,47{{t}^{2}}-11493,5t+35493\left( 4\le t\le 19 \right)$, trong đó $t$ là đại diện cho năm, với $t=4$ tương ứng với năm 2004

Từ năm 2004 đến năm 2019 doanh thu $R\left( t \right)$ (tính bằng triệu đô la) của McDonald’s có thể được mô hình hóa bởi $R\left( t \right)=-130,769{{t}^{3}}+2296,47{{t}^{2}}-11493,5t+35493\left( 4\le t\le 19 \right)$, trong đó $t$ là đại diện cho năm, với $t=4$ tương ứng với năm 2004. Biết rằng ${R}’\left( t \right)$ là hàm tốc độ doanh thu theo thời gian. Tốc độ thay đổi doanh thu của McDonald’s lớn nhất vào năm nào? (Kết quả làm tròn đến hàng đơn vị, tính theo triệu đô la mỗi năm).

Lời giải

Đáp án: $2006$.

Ta có hàm tốc độ doanh thu là ${R}’\left( t \right)=-392,307{{t}^{2}}+4592,94t-11493,5$.

${R}”\left( t \right)=-784,614t+4592,94=0$ $\Leftrightarrow t\approx 6$ (nhận).

Ta có bảng biến thiên của hàm số

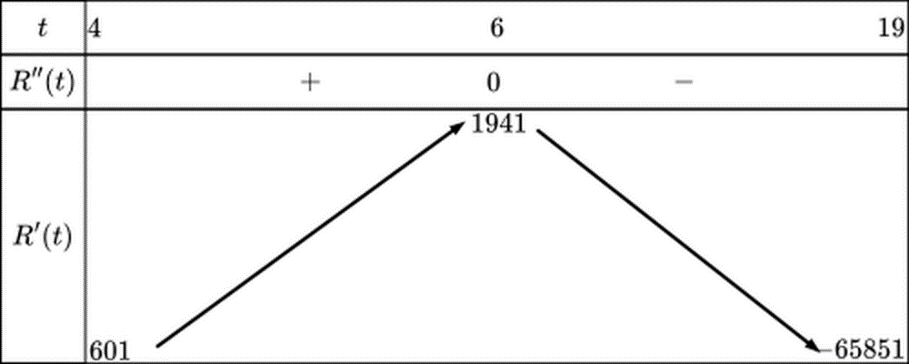
Dựa bào bảng biến thiên ta thấy rằng tốc độ thay đổi doanh thu của McDonald’s lớn nhất vào năm 2006 (tương ứng với $t=6$ ).