Trắc nghiệm Đơn điệu hàm số 12 – Đồ thị

Câu 1: Cho hàm số $y=\dfrac{ax+b}{cx+d},(ad-bc\neq 0)$. Có đồ thị như hình dưới đây:

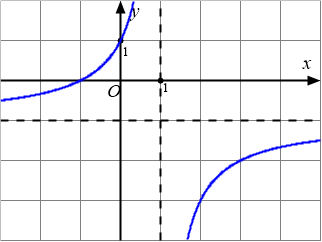
Chọn khẳng định đúng?
*A. $y^{\prime}{>}0,\forall x \neq 1$. B. $y^{\prime}{<}0,\forall x \neq 1$. *C. $y^{\prime}{<}0,\forall x \in \mathbb{R}$. D. $y^{\prime}{>}0,\forall x \in \mathbb{R}$.

Câu 2: Cho hàm số $y=\dfrac{ax+b}{cx+d},(ad-bc\neq 0)$. Có đồ thị như hình dưới đây:

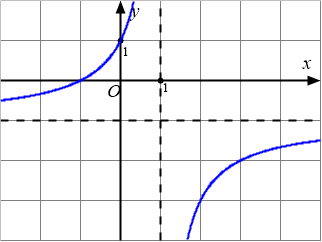
Hàm số $y=f(x)$ đồng biến trên?
*A. $(1;+\infty)$. B. $\mathbb{R}\backslash \left\{ 1 \right\}$. C. $(-1;+\infty)$. D. $(-\infty; 3)$.

Câu 3: Hàm số $y=f(x)=ax^4+bx^2+c,a\neq 0$ có đồ thị như hình dưới đây:

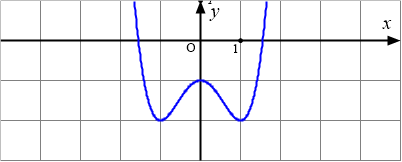
Chọn phát biểu đúng?
*A. Hàm số $y=f(x)$ đồng biến trên $(1;+\infty)$. B. Hàm số $y=f(x)$ đồng biến trên $(-1;+\infty)$.
*C. Hàm số $y=f(x)$ nghịch biến trên $(-\infty;0)$. D. Hàm số $y=f(x)$ nghịch biến trên $(-\infty;1)$.

Câu 4: Cho hàm số $y=f'(x)$ có đồ thị như hình dưới đây:

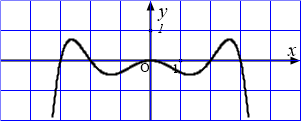
Hàm số $y=f(x)$ đồng biến trên khoảng nào?
*A. $(2;3)$. B. $(0;2)$. C. $(-2;0)$. D. $(1;3)$.

Câu 5: Cho hàm số $y=ax^3+bx^2+cx+d,(a\neq 0)$ có đồ thị như hình dưới đây:

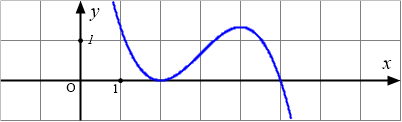
Hàm số $y=f(x)$ nghịch biến trên khoảng nào?
*A. $(-\infty;2)$. B. $(-\infty ;4)$. C. $(2;+\infty)$. D. $(2;4)$.

Câu 6: Cho hàm số $y=f(x)$. Hàm số $y=f^{\prime}(x)=ax^2+bx+c,(a\neq 0)$ có đồ thị như hình dưới đây:

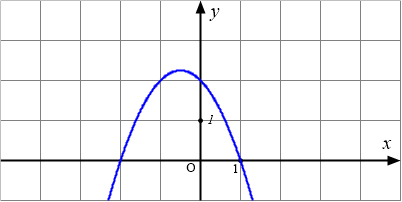
Chọn phát biểu sai?
*A. Hàm số $y=f(x)$ nghịch biến trên $\left(-\dfrac{1}{2};+\infty\right)$.
*B. Hàm số $y=f(x)$ đồng biến trên $(-2;1)$.
*C. Hàm số $y=f(x)$ nghịch biến trên $(-\infty;-2)$.
*D. Hàm số $y=f(x)$ nghịch biến biến trên $(1;+\infty)$.