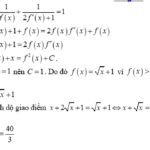Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(\left[ {0; + \infty } \right)\) thỏa mãn \[f\left( 0 \right) = 1\], \[f\left( x \right) > 0,\forall x \in \left[ {0; + \infty } \right)\] và\(\frac{1}{{f\left( x \right)}} + \frac{1}{{2f'\left( x \right) + 1}} = 1,\forall x \in \left[ {0; + \infty } \right)\). Diện tích hình phẳng giới hạn bởi các đường \(y = f(x)\) , \(y = … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) có đạo hàm trên \(\left[ {0; + \infty } \right)\) thỏa mãn \(f\left( 0 \right) = 1\), \(f\left( x \right) > 0,\forall x \in \left[ {0; + \infty } \right)\) và\(\frac{1}{{f\left( x \right)}} + \frac{1}{{2f’\left( x \right) + 1}} = 1,\forall x \in \left[ {0; + \infty } \right)\). Diện tích hình phẳng giới hạn bởi các đường \(y = f(x)\) , \(y = {\left[ {f(x)} \right]^2}\) và đường thẳng \(x = 4\) bằng
Ung dung tich phan
Bài tập luyện tập ỨNG DỤNG TÍCH PHÂN – 2023
Bài tập luyện tập ỨNG DỤNG TÍCH PHÂN – 2023 ========== booktoan.com chia sẻ Bài tập luyện tập ỨNG DỤNG TÍCH PHÂN – 2023. Đề có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân. Chúc các em thành công và đạt kết quả cao trong học toán 12 năm học 2022 – 2023. NGUỒN: BOOKTOAN.COM ———– xem file de thi — ============= xem online file docx … [Đọc thêm...] vềBài tập luyện tập ỨNG DỤNG TÍCH PHÂN – 2023
Cho hàm số \(f(x) = {x^4} + a{x^2} + bx + 1\) và \(g(x) = c{x^2} + dx + 3\) với \((a,b,c,d \in \mathbb{R})\). Biết rằng đồ thị của hàm số \(y = f(x)\) và \(y = g(x)\) cắt nhau tại hai điểm có hoành độ lần lượt là \( – 2;1\). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
Cho hàm số \(f(x) = {x^4} + a{x^2} + bx + 1\) và \(g(x) = c{x^2} + dx + 3\) với \((a,b,c,d \in \mathbb{R})\). Biết rằng đồ thị của hàm số \(y = f(x)\) và \(y = g(x)\) cắt nhau tại hai điểm có hoành độ lần lượt là \( - 2;1\). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng A. \(\frac{{45}}{5}\) B. \(2\) C. \(\frac{{99}}{{10}}\) … [Đọc thêm...] vềCho hàm số \(f(x) = {x^4} + a{x^2} + bx + 1\) và \(g(x) = c{x^2} + dx + 3\) với \((a,b,c,d \in \mathbb{R})\). Biết rằng đồ thị của hàm số \(y = f(x)\) và \(y = g(x)\) cắt nhau tại hai điểm có hoành độ lần lượt là \( – 2;1\). Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng
Cho hàm số \(f(x) = 3{x^3} + b{x^2} + cx + d\) với \(b,c,d \in \mathbb{R}\). Biết hàm số \(g(x) = f(x) + f'(x) + f”(x)\) có hai giá trị cực trị là \( – 12;6\). Diện tích hình phẳng giới hạn bởi các đường \(y = \frac{{f(x)}}{{g(x) + 18}}\) và \(y = 1\) bằng
Cho hàm số \(f(x) = 3{x^3} + b{x^2} + cx + d\) với \(b,c,d \in \mathbb{R}\). Biết hàm số \(g(x) = f(x) + f'(x) + f''(x)\) có hai giá trị cực trị là \( - 12;6\). Diện tích hình phẳng giới hạn bởi các đường \(y = \frac{{f(x)}}{{g(x) + 18}}\) và \(y = 1\) bằng A. \(2\ln 3\) B. \(\ln 6\) C. \(2\ln 2\) D. \(\ln … [Đọc thêm...] vềCho hàm số \(f(x) = 3{x^3} + b{x^2} + cx + d\) với \(b,c,d \in \mathbb{R}\). Biết hàm số \(g(x) = f(x) + f'(x) + f”(x)\) có hai giá trị cực trị là \( – 12;6\). Diện tích hình phẳng giới hạn bởi các đường \(y = \frac{{f(x)}}{{g(x) + 18}}\) và \(y = 1\) bằng
Cho hàm số\(f(x) = {x^4} + a{x^3} + b{x^2} + cx + d\) với \(a,b,c,d \in \mathbb{R}\). Diện tích hình phẳng giới hạn bởi các đường \(y = \frac{{f(x)}}{{g(x) + 24}}\) và \(y = 1\) bằng
Cho hàm số\(f(x) = {x^4} + a{x^3} + b{x^2} + cx + d\) với \(a,b,c,d \in \mathbb{R}\). Biết hàm số\(g(x) = f(x) + {f^\prime }(x) + {f^{\prime \prime }}(x) + {f^{\prime \prime \prime }}(x)\) có ba giá trị cực trị là \( - 14;4;6\). Diện tích hình phẳng giới hạn bởi các đường \(y = \frac{{f(x)}}{{g(x) + 24}}\) và \(y = 1\) bằng A. \(2\ln 3\) B. … [Đọc thêm...] vềCho hàm số\(f(x) = {x^4} + a{x^3} + b{x^2} + cx + d\) với \(a,b,c,d \in \mathbb{R}\). Diện tích hình phẳng giới hạn bởi các đường \(y = \frac{{f(x)}}{{g(x) + 24}}\) và \(y = 1\) bằng
Cho \(y = f(x) = a{x^2} + bx + c\) với \(a,b,c \in \mathbb{R}\). Biết rằng hàm số \(g(x) = f(x) \cdot {e^{ – x}}\) có hai giá trị cực trị là \(5\) và \( – 3\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(g(x)\) và \(h(x) = (2ax + b) \cdot {{\rm{e}}^{ – x}}\) bằng
Cho \(y = f(x) = a{x^2} + bx + c\) với \(a,b,c \in \mathbb{R}\). Biết rằng hàm số \(g(x) = f(x) \cdot {e^{ - x}}\) có hai giá trị cực trị là \(5\) và \( - 3\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(g(x)\) và \(h(x) = (2ax + b) \cdot {{\rm{e}}^{ - x}}\) bằng A. \(2\) B. \(8\) C. \({{\rm{e}}^5} - {{\rm{e}}^{ - 3}}\) D. \({{\rm{e}}^5} - {{\rm{e}}^3}\) Lời giải Ta … [Đọc thêm...] vềCho \(y = f(x) = a{x^2} + bx + c\) với \(a,b,c \in \mathbb{R}\). Biết rằng hàm số \(g(x) = f(x) \cdot {e^{ – x}}\) có hai giá trị cực trị là \(5\) và \( – 3\). Diện tích hình phẳng giới hạn bởi đồ thị hàm số \(g(x)\) và \(h(x) = (2ax + b) \cdot {{\rm{e}}^{ – x}}\) bằng
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Biết diện tích phần gạch chéo trên hình bằng 6.
Giá trị của biểu thức \(T = 3\int\limits_{ – 1}^1 {f\left( {2x – 1} \right)} dx + \int\limits_0^1 {f’\left( {x + 2} \right)} dx + \int\limits_1^2 {f’\left( x \right)} dx\) bằng.
Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Biết diện tích phần gạch chéo trên hình bằng 6. Giá trị của biểu thức \(T = 3\int\limits_{ - 1}^1 {f\left( {2x - 1} \right)} dx + \int\limits_0^1 {f'\left( {x + 2} \right)} dx + \int\limits_1^2 {f'\left( x \right)} dx\) bằng. A. \( - 8\) B. \(6\). C. … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Biết diện tích phần gạch chéo trên hình bằng 6.
Giá trị của biểu thức \(T = 3\int\limits_{ – 1}^1 {f\left( {2x – 1} \right)} dx + \int\limits_0^1 {f’\left( {x + 2} \right)} dx + \int\limits_1^2 {f’\left( x \right)} dx\) bằng.
Cho hàm số \(f(x)\) có đạo hàm liên tục trên đoạn \(\left[ {1;3} \right]\) và thỏa mãn \(f(1) = – \frac{1}{2}\) và
\(\frac{{f(x) – xf'(x)}}{{{f^2}(x)}} = 3{x^2} – 1,\forall x \in [1;3].\) Giá trị của tích phân \(\int\limits_2^3 {f'(x)dx} \) bằng
Câu hỏi: Cho hàm số \(f(x)\) có đạo hàm liên tục trên đoạn \(\left[ {1;3} \right]\) và thỏa mãn \(f(1) = - \frac{1}{2}\) và \(\frac{{f(x) - xf'(x)}}{{{f^2}(x)}} = 3{x^2} - 1,\forall x \in [1;3].\) Giá trị của tích phân \(\int\limits_2^3 {f'(x)dx} \) bằng A. \(\frac{{ - 4}}{{11}}\). B. \(\frac{{ - 23}}{{308}}\). C. \(\frac{{ - 23}}{{11}}\). D. … [Đọc thêm...] vềCho hàm số \(f(x)\) có đạo hàm liên tục trên đoạn \(\left[ {1;3} \right]\) và thỏa mãn \(f(1) = – \frac{1}{2}\) và
\(\frac{{f(x) – xf'(x)}}{{{f^2}(x)}} = 3{x^2} – 1,\forall x \in [1;3].\) Giá trị của tích phân \(\int\limits_2^3 {f'(x)dx} \) bằng
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x – 1}&{{\rm{khi}}x \ge 3}\\{{x^2} – 7}&{{\rm{khi}}x < 3}\end{array}} \right.\). Tích phân \(\mathop \smallint \limits_0^{{\rm{ln}}5} f\left( {{e^x} + 1} \right){e^x}dx\) bằng
Câu hỏi: Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x - 1}&{{\rm{khi}}x \ge 3}\\{{x^2} - 7}&{{\rm{khi}}x < 3}\end{array}} \right.\). Tích phân \(\mathop \smallint \limits_0^{{\rm{ln}}5} f\left( {{e^x} + 1} \right){e^x}dx\) bằng A. \(\frac{{59}}{6}\). B. \(\frac{{43}}{{12}}\). C. \( - \frac{{59}}{6}\). D. \(\frac{7}{3}\) . … [Đọc thêm...] vềCho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}{x – 1}&{{\rm{khi}}x \ge 3}\\{{x^2} – 7}&{{\rm{khi}}x < 3}\end{array}} \right.\). Tích phân \(\mathop \smallint \limits_0^{{\rm{ln}}5} f\left( {{e^x} + 1} \right){e^x}dx\) bằng
Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có \(\int\limits_0^3 {f\left( x \right){\rm{d}}x} = 8\) và \(\int\limits_0^5 {f(x){\rm{d}}x} = 4\). Tính \(\int\limits_{ – 1}^1 {f\left( {\left| {4x – 1} \right|} \right){\rm{d}}x} \)
Câu hỏi: Cho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có \(\int\limits_0^3 {f\left( x \right){\rm{d}}x} = 8\) và \(\int\limits_0^5 {f(x){\rm{d}}x} = 4\). Tính \(\int\limits_{ - 1}^1 {f\left( {\left| {4x - 1} \right|} \right){\rm{d}}x} \) A. \(3\). B. \(\frac{{11}}{4}\). C. \(\frac{9}{4}\). D. \(6\). LỜI GIẢI CHI TIẾT Ta có: … [Đọc thêm...] vềCho hàm số \(f(x)\) liên tục trên \(\mathbb{R}\) và có \(\int\limits_0^3 {f\left( x \right){\rm{d}}x} = 8\) và \(\int\limits_0^5 {f(x){\rm{d}}x} = 4\). Tính \(\int\limits_{ – 1}^1 {f\left( {\left| {4x – 1} \right|} \right){\rm{d}}x} \)