MU - LOGA VDC

Cho \(0 \le x \le 2022\) và \({\log _2}\left( {2x + 2} \right) + x – 3y = {8^y}\). Có bao nhiêu cặp \(\left( {x;y} \right)\) nguyên thỏa mãn các điều kiện trên?

Ngày 11/06/2023 Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, Phuong trinh logarit, VDC Toan 2023

Cho \(0 \le x \le 2022\) và \({\log _2}\left( {2x + 2} \right) + x - 3y = {8^y}\). Có bao nhiêu cặp \(\left( {x;y} \right)\) nguyên thỏa mãn các điều kiện trên? A. 1. B. 2022. C. 2021. D. 4. Lời giải: Ta có : \({\log _2}\left( {2x + 2} \right) + x - 3y = {8^y}\) \(\begin{array}{l} \Leftrightarrow x + 1 + {\log _2}\left( {x + 1} \right) = {8^y} + 3y\\ … [Đọc thêm...] vềCho \(0 \le x \le 2022\) và \({\log _2}\left( {2x + 2} \right) + x – 3y = {8^y}\). Có bao nhiêu cặp \(\left( {x;y} \right)\) nguyên thỏa mãn các điều kiện trên?

. Tập nghiệm của bất phương trình \({\log _{\frac{1}{2}}}\left( {x – 1} \right) + {\log _2}\left( {x – 1} \right) + {\log _2}\left( {x + 3} \right) \ge 1\) là

Ngày 11/06/2023 Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:MU - LOGA VDC, Phuong trinh logarit

. Tập nghiệm của bất phương trình \({\log _{\frac{1}{2}}}\left( {x - 1} \right) + {\log _2}\left( {x - 1} \right) + {\log _2}\left( {x + 3} \right) \ge 1\) là A. \(\left[ {1;\, + \infty } \right)\). B. \(\left[ { - 1;\, + \infty } \right)\). C. \(\left( {1;\, + \infty } \right)\). D. \(\left( { - 3;\, + \infty } \right)\). Lời giải: Điều kiện: \(x > … [Đọc thêm...] về. Tập nghiệm của bất phương trình \({\log _{\frac{1}{2}}}\left( {x – 1} \right) + {\log _2}\left( {x – 1} \right) + {\log _2}\left( {x + 3} \right) \ge 1\) là

Có bao nhiêu số nguyên dương \(x,x \le 2023\) sao cho tồn tại số nguyên \(y\)thỏa mãn \(x\left( {{2^y} + y – 1} \right) = 2 – {\log _2}{x^x}\)

Ngày 11/06/2023 Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:MU - LOGA VDC, Phuong trinh logarit

Có bao nhiêu số nguyên dương \(x,x \le 2023\) sao cho tồn tại số nguyên \(y\)thỏa mãn \(x\left( {{2^y} + y - 1} \right) = 2 - {\log _2}{x^x}\) A. 12. B. 9. C. 10. D. 11. Lời giải: Ta có: \(x\left( {{2^y} + y - 1} \right) = 2 - {\log _2}{x^x} \Leftrightarrow x{\log _2}x + x\left( {{2^y} + y - 1} \right) = 2.\) Đặt \(t = {\log _2}x \Leftrightarrow x = … [Đọc thêm...] vềCó bao nhiêu số nguyên dương \(x,x \le 2023\) sao cho tồn tại số nguyên \(y\)thỏa mãn \(x\left( {{2^y} + y – 1} \right) = 2 – {\log _2}{x^x}\)

Cho các số thực dương \(a\), \(b\) thỏa mãn \(\ln \frac{{2 – 2ab}}{{a + b}} = 2ab + a + b – 2\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của \(P = a + 2b\).

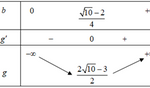
Ngày 05/03/2023 Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, VDC Toan 2023

Cho các số thực dương \(a\), \(b\) thỏa mãn \(\ln \frac{{2 - 2ab}}{{a + b}} = 2ab + a + b - 2\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của \(P = a + 2b\). A. \({P_{\min }} = \frac{{2\sqrt {10} - 3}}{2}\). B. \({P_{\min }} = \frac{{3\sqrt {10} - 7}}{2}\). C. \({P_{\min }} = \frac{{2\sqrt {10} - 1}}{2}\). D. \({P_{\min }} = \frac{{2\sqrt {10} - 5}}{2}\). Lời giải Điều … [Đọc thêm...] vềCho các số thực dương \(a\), \(b\) thỏa mãn \(\ln \frac{{2 – 2ab}}{{a + b}} = 2ab + a + b – 2\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của \(P = a + 2b\).

\({2^{2{x^2} – 15x + 100}} – {2^{{x^2} + 10x – 50}} + {x^2} – 25x + 150 < 0\) là

Ngày 03/03/2023 Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, VDC Toan 2023

\({2^{2{x^2} - 15x + 100}} - {2^{{x^2} + 10x - 50}} + {x^2} - 25x + 150 < 0\) là A. \(4\). B. \(6.\) C. \(3\). D. \(5\). Lời giải Ta có \({2^{2{x^2} - 15x + 100}} - {2^{{x^2} + 10x - 50}} + {x^2} - 25x + 150 < 0\) \( \Leftrightarrow {2^{2{x^2} - 15x + 100}} - {2^{{x^2} + 10x - 50}} + 2{x^2} - 15x + 100 - \left( {{x^2} + 10x - 50} \right) < … [Đọc thêm...] về\({2^{2{x^2} – 15x + 100}} – {2^{{x^2} + 10x – 50}} + {x^2} – 25x + 150 < 0\) là

Cho hai số thực dương \(x,y\) thay đổi và thỏa mãn hệ thức\(4 + \ln \frac{{2x + 2y + 1}}{{5xy}} = 20xy – \left( {8x + 8y} \right)\).Giá trị nhỏ nhất của biểu thức \(P = xy + 9\) bằng

Ngày 02/03/2023 Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, VDC Toan 2023

Cho hai số thực dương \(x,y\) thay đổi và thỏa mãn hệ thức \(4 + \ln \frac{{2x + 2y + 1}}{{5xy}} = 20xy - \left( {8x + 8y} \right)\). Giá trị nhỏ nhất của biểu thức \(P = xy + 9\) bằng A. \(m = 11.\) B. \(m = 10.\) C. \(m = 12 \cdot \) D. \(m = \frac{{19}}{2} \cdot \) Lời giải: Ta có \(4 + \ln \frac{{2x + 2y + 1}}{{5xy}} = 20xy - 8x - 8y\,\,\, \Leftrightarrow \ln \left( … [Đọc thêm...] vềCho hai số thực dương \(x,y\) thay đổi và thỏa mãn hệ thức\(4 + \ln \frac{{2x + 2y + 1}}{{5xy}} = 20xy – \left( {8x + 8y} \right)\).Giá trị nhỏ nhất của biểu thức \(P = xy + 9\) bằng

Tập nghiệm của bất phương trình \({3^{3x}} – {5^{3x}} + 3\left( {{3^x} – {5^x}} \right) > 0\) là

Ngày 28/02/2023 Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, VDC Toan 2023

Tập nghiệm của bất phương trình \({3^{3x}} - {5^{3x}} + 3\left( {{3^x} - {5^x}} \right) > 0\) là A. \(\left( { - \infty ;0} \right)\). B. \(\left( { - \infty ;0} \right]\). C. \(\left( {0; + \infty } \right)\). D. \(\left[ {0; + \infty } \right)\). Lời giải Bất phương trình đã cho tương đương với \({3^{3x}} + {3.3^x} > {5^{3x}} + {3.5^x} \Leftrightarrow f\left( {{3^x}} … [Đọc thêm...] vềTập nghiệm của bất phương trình \({3^{3x}} – {5^{3x}} + 3\left( {{3^x} – {5^x}} \right) > 0\) là

Cho các số thực \(x,y\) thỏa mãn \(0 \le x,y \le 1\) và \({\log _2}\frac{{x + y}}{{2 – xy}} + 2\left( {x + 1} \right)\left( {y + 1} \right) – 6 = 0\). Tìm giá trị lớn nhất của \(P = 3x + y\).

Ngày 28/02/2023 Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, VDC Toan 2023

Cho các số thực \(x,y\) thỏa mãn \(0 \le x,y \le 1\) và \({\log _2}\frac{{x + y}}{{2 - xy}} + 2\left( {x + 1} \right)\left( {y + 1} \right) - 6 = 0\). Tìm giá trị lớn nhất của \(P = 3x + y\). A. \(3\). B. \(\frac{7}{2}\). C. \(4\). D. \(\frac{5}{2}\). Lời giải Với điều kiện \(\left\{ \begin{array}{l}0 \le x,y \le 1\\x + y > 0\end{array} \right.\) ta có: \({\log _2}\frac{{x … [Đọc thêm...] vềCho các số thực \(x,y\) thỏa mãn \(0 \le x,y \le 1\) và \({\log _2}\frac{{x + y}}{{2 – xy}} + 2\left( {x + 1} \right)\left( {y + 1} \right) – 6 = 0\). Tìm giá trị lớn nhất của \(P = 3x + y\).

Tập nghiệm của bất phương trình \({\log _2}\left( {{x^2} + 3} \right) – {\log _2}x + {x^2} – 4x + 1 \le 0\) là

Ngày 27/02/2023 Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:HAM DAC TRUNG MU LOGA, MU - LOGA VDC, VDC Toan 2023

Tập nghiệm của bất phương trình \({\log _2}\left( {{x^2} + 3} \right) - {\log _2}x + {x^2} - 4x + 1 \le 0\) là A. \(S = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\). B. \(\left[ { - 1;3} \right]\). C. \(\left[ {1; + \infty } \right)\). D. \(S = \left[ {1;3} \right]\). Lời giải Điều kiện: \(x > 0\). Ta có \({\log _2}\left( {{x^2} + 3} \right) - {\log … [Đọc thêm...] vềTập nghiệm của bất phương trình \({\log _2}\left( {{x^2} + 3} \right) – {\log _2}x + {x^2} – 4x + 1 \le 0\) là