Có bao nhiêu giá trị nguyên của tham số \(m \in \left( { - 10;10} \right)\) sao cho ứng với mỗi \(m\), hàm số \(y = \frac{{\left( {m + 1} \right)x + 18}}{{3x + 2m - 1}}\) nghịch biến trên khoảng \(\left( {3;\,\,7} \right)\)? A. \(8\). B. \(10\). C. \(11\). D. \(9\). Lời giải: Điều kiện: \(3x + 2m - 1 \ne 0 \Leftrightarrow x … [Đọc thêm...] vềCó bao nhiêu giá trị nguyên của tham số \(m \in \left( { – 10;10} \right)\) sao cho ứng với mỗi \(m\), hàm số \(y = \frac{{\left( {m + 1} \right)x + 18}}{{3x + 2m – 1}}\) nghịch biến trên khoảng \(\left( {3;\,\,7} \right)\)?
Don dieu ham hop
Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) có đồ thị hàm số như hình dưới đây. Hàm số \(g\left( x \right) = f\left( {{x^2} + 3x + 1} \right)\) đồng biến trên khoảng nào?
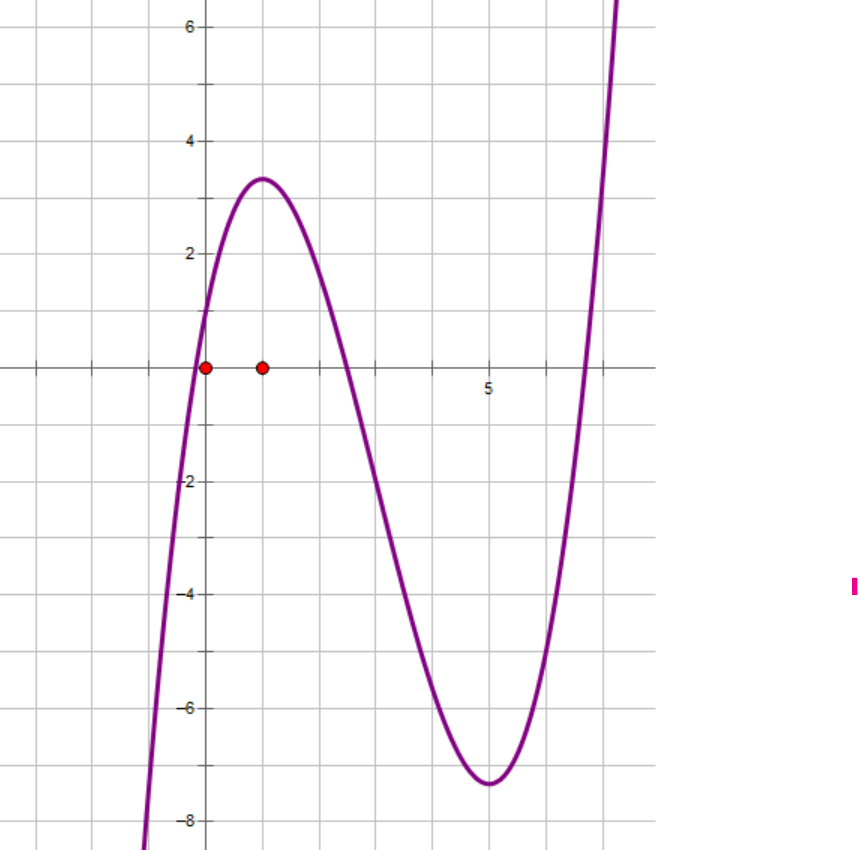
Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) có đồ thị hàm số như hình dưới đây. Hàm số \(g\left( x \right) = f\left( {{x^2} + 3x + 1} \right)\) đồng biến trên khoảng nào? A. \(\left( { - 4; - 3} \right)\). B. \(\left( { - 2;0} \right).\) C. \(\left( { - \frac{3}{2};1} \right)\) D. \(\left( { - 3; - 2} … [Đọc thêm...] về Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) có đồ thị hàm số như hình dưới đây. Hàm số \(g\left( x \right) = f\left( {{x^2} + 3x + 1} \right)\) đồng biến trên khoảng nào?
Cho hàm số \(f(x) = \frac{{\left( {m + 1} \right)\sqrt { – 2x + 3} – 1}}{{ – \sqrt { – 2x + 3} + \frac{2}{m}}}\) (\(m\) là tham số thực). Tập hợp tất cả các giá trị của \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( { – \frac{1}{2};\,\,1} \right)\) là \(\left( { – \infty ;\,\,a} \right) \cup \left( {b;\,\,c} \right] \cup \left[ {d;\,\, + \infty } \right)\). Giá trị của biểu thức \(a – b + c – d\) bằng.
Cho hàm số \(f(x) = \frac{{\left( {m + 1} \right)\sqrt { - 2x + 3} - 1}}{{ - \sqrt { - 2x + 3} + \frac{2}{m}}}\) (\(m\) là tham số thực). Tập hợp tất cả các giá trị của \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( { - \frac{1}{2};\,\,1} \right)\) là \(\left( { - \infty ;\,\,a} \right) \cup \left( {b;\,\,c} \right] \cup \left[ {d;\,\, + \infty } \right)\). … [Đọc thêm...] vềCho hàm số \(f(x) = \frac{{\left( {m + 1} \right)\sqrt { – 2x + 3} – 1}}{{ – \sqrt { – 2x + 3} + \frac{2}{m}}}\) (\(m\) là tham số thực). Tập hợp tất cả các giá trị của \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( { – \frac{1}{2};\,\,1} \right)\) là \(\left( { – \infty ;\,\,a} \right) \cup \left( {b;\,\,c} \right] \cup \left[ {d;\,\, + \infty } \right)\). Giá trị của biểu thức \(a – b + c – d\) bằng.
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\). Biết rằng đồ thị hàm \(y = f’\left( x \right)\)được cho như hình vẽ bên.
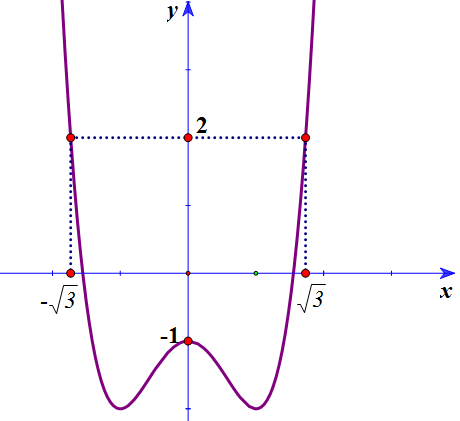
Giá trị nhỏ nhất của hàm số \(g\left( x \right) = 3f\left( {2x + 1} \right) – 8{x^3} – 12{x^2} + 2\) trên đoạn \(\left[ { – 1;1} \right]\) bằng:
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\). Biết rằng đồ thị hàm \(y = f'\left( x \right)\)được cho như hình vẽ bên. Giá trị nhỏ nhất của hàm số \(g\left( x \right) = 3f\left( {2x + 1} \right) - 8{x^3} - 12{x^2} + 2\) trên đoạn \(\left[ { - 1;1} \right]\) bằng: A. \(3f\left( { - 1} \right) - 2\). B. \(3f\left( 0 … [Đọc thêm...] về Cho hàm số \(y = f\left( x \right)\)liên tục trên \(\mathbb{R}\). Biết rằng đồ thị hàm \(y = f’\left( x \right)\)được cho như hình vẽ bên.
Giá trị nhỏ nhất của hàm số \(g\left( x \right) = 3f\left( {2x + 1} \right) – 8{x^3} – 12{x^2} + 2\) trên đoạn \(\left[ { – 1;1} \right]\) bằng:
Tìm tập các giá trị của \(m\) để hàm số \(y = \frac{{\ln x – m}}{{m\ln x – 4}}\) đồng biến trên khoảng \(\left( {{\rm{e}}; + \infty } \right)\).
Tìm tập các giá trị của \(m\) để hàm số \(y = \frac{{\ln x - m}}{{m\ln x - 4}}\) đồng biến trên khoảng \(\left( {{\rm{e}}; + \infty } \right)\). A. \(\left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\). B. \(\left( { - \infty ; - 2} \right) \cup \left[ {4; + \infty } \right)\). C. \(\left( { - \infty ; - 2} \right)\). D. … [Đọc thêm...] vềTìm tập các giá trị của \(m\) để hàm số \(y = \frac{{\ln x – m}}{{m\ln x – 4}}\) đồng biến trên khoảng \(\left( {{\rm{e}}; + \infty } \right)\).
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { – 2;25} \right]\) sao cho ứng với mỗi \(m\), hàm số \(y = \frac{{{x^2} + 5x – m – 1}}{{5x – m}}\) nghịch biến trên khoảng \(\left( {1;4} \right)\).
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2;25} \right]\) sao cho ứng với mỗi \(m\), hàm số \(y = \frac{{{x^2} + 5x - m - 1}}{{5x - m}}\) nghịch biến trên khoảng \(\left( {1;4} \right)\). A. \(8\). B. \(15\). C. \(14\). D. \(6\). Lời giải: Tập xác định: \(D = \mathbb{R}\backslash \left\{ {\frac{m}{5}} … [Đọc thêm...] vềCó bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { – 2;25} \right]\) sao cho ứng với mỗi \(m\), hàm số \(y = \frac{{{x^2} + 5x – m – 1}}{{5x – m}}\) nghịch biến trên khoảng \(\left( {1;4} \right)\).
Cho hàm số \(y = \frac{{\ln x – 6}}{{\ln x – 3m}}\) với \(m\) là tham số. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số đồng biến trên khoảng \(\left( {1;{\rm{e}}} \right)\). Tìm số phần tử của \(S\).
Cho hàm số \(y = \frac{{\ln x - 6}}{{\ln x - 3m}}\) với \(m\) là tham số. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số đồng biến trên khoảng \(\left( {1;{\rm{e}}} \right)\). Tìm số phần tử của \(S\). A. \(2\). B.\(4\). C. \(3\). D. \(1\). Lời giải: Điều kiện \(\ln x - 3m \ne 0\)\( \Leftrightarrow m \ne … [Đọc thêm...] về Cho hàm số \(y = \frac{{\ln x – 6}}{{\ln x – 3m}}\) với \(m\) là tham số. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số đồng biến trên khoảng \(\left( {1;{\rm{e}}} \right)\). Tìm số phần tử của \(S\).
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình bên. Có bao nhiêu số nguyên \(m\) để hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} + mx + 8 – m} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\)?
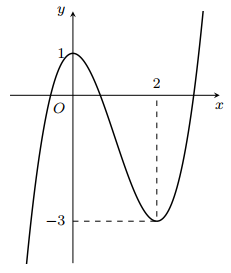
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình bên. Có bao nhiêu số nguyên \(m\) để hàm số \(g\left( x \right) = f\left( {{x^3} - 3{x^2} + mx + 8 - m} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\)? A. \(5\). B. \(6\). C. \(4\). D. \(3\). Lời giải: Ta có \(g'\left( x \right) = \left( … [Đọc thêm...] về Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị như hình bên. Có bao nhiêu số nguyên \(m\) để hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} + mx + 8 – m} \right)\) đồng biến trên \(\left( {0; + \infty } \right)\)?
Cho hàm số \(y = \frac{{{x^2} + x + m}}{{x – 1}}\), (\(m\) là tham số). Tìm tất cả các giá trị thực của tham số \(m\) để hàm số có hai cực trị \(a,\,b\) thỏa mãn \({a^2} + {b^2} = 10\).
Cho hàm số \(y = \frac{{{x^2} + x + m}}{{x - 1}}\), (\(m\) là tham số). Tìm tất cả các giá trị thực của tham số \(m\) để hàm số có hai cực trị \(a,\,b\) thỏa mãn \({a^2} + {b^2} = 10\). A. \(m = - 3\). B. \(m = 2\). C. \(m = \frac{7}{2}\). D. \(m = 1\) Lời giải: Ta có \(y' = \frac{{{x^2} - 2x - m - 1}}{{{{\left( … [Đọc thêm...] về Cho hàm số \(y = \frac{{{x^2} + x + m}}{{x – 1}}\), (\(m\) là tham số). Tìm tất cả các giá trị thực của tham số \(m\) để hàm số có hai cực trị \(a,\,b\) thỏa mãn \({a^2} + {b^2} = 10\).
Cho hàm số \(y = {x^3} – 3m{x^2} + 3\left( {{m^2} – 1} \right)x + 2020\). Có tất cả bao nhiêu giá trị nguyên của \(m\) sao cho hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\)?
Cho hàm số \(y = {x^3} - 3m{x^2} + 3\left( {{m^2} - 1} \right)x + 2020\). Có tất cả bao nhiêu giá trị nguyên của \(m\) sao cho hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\)? A. \(2\). B. \(1\). C. 4. D. \(3\). Lời giải: Ta có \(y' = 3{x^2} - 6mx + 3\left( {{m^2} - 1} \right) = 0 \Leftrightarrow … [Đọc thêm...] về Cho hàm số \(y = {x^3} – 3m{x^2} + 3\left( {{m^2} – 1} \right)x + 2020\). Có tất cả bao nhiêu giá trị nguyên của \(m\) sao cho hàm số có giá trị nhỏ nhất trên khoảng \(\left( {0; + \infty } \right)\)?
