Don dieu ham hop

Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f\left( x \right)\) như hình bên dưới. Hàm số \(g\left( x \right) = f\left( {{x^2} – x} \right)\) có bao nhiêu cực trị

Ngày 20/05/2024 Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:Don dieu ham hop, don dieu VD, Tim m de tang giam tren khoang

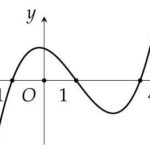
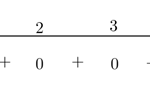Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f\left( x \right)\) như hình bên dưới. Hàm số \(g\left( x \right) = f\left( {{x^2} - x} \right)\) có bao nhiêu cực trị A. \(2\). B. \(3\). C. \(4\). D. \(5\). Lời giải: Từ đồ thị \(f\left( x \right)\) ta có \(f'\left( x \right) = 0 \Leftrightarrow \left[ … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đồ thị hàm số \(y = f\left( x \right)\) như hình bên dưới. Hàm số \(g\left( x \right) = f\left( {{x^2} – x} \right)\) có bao nhiêu cực trị

Cho hàm số $f(x)$ có đồ thị hàm số $f^{\prime}(x)$ như hình vẽ dưới đây. Có bao nhiêu số nguyên $m>-10$ để hàm số $y=f(x+m)$ nghịch biến trên $(0 ; 2)$ ?

Ngày 13/12/2023 Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:Don dieu ham hop, VDC Toan 2023

Cho hàm số $f(x)$ có đồ thị hàm số $f^{\prime}(x)$ như hình vẽ dưới đây. Có bao nhiêu số nguyên $m>-10$ để hàm số $y=f(x+m)$ nghịch biến trên $(0 ; 2)$ ? A. 7 . B. 5 . C. 9 . D. 2 . Lời giải. Yêu cầu bài toán $$ \begin{aligned} & \Leftrightarrow \quad y^{\prime}=f^{\prime}(x+m) \leq 0, \forall x \in(0 ; 2) \\ & \Leftrightarrow\left[\begin{array}{l} x+m \leq-1 … [Đọc thêm...] vềCho hàm số $f(x)$ có đồ thị hàm số $f^{\prime}(x)$ như hình vẽ dưới đây. Có bao nhiêu số nguyên $m>-10$ để hàm số $y=f(x+m)$ nghịch biến trên $(0 ; 2)$ ?

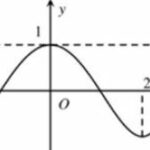
Hàm số \(y = f\left( {2x – 1} \right) + \dfrac{{{x^3}}}{3} + {x^2} – 2x\) nghịch biến trên khoảng nào sau đây:

Ngày 15/05/2022 Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:Don dieu ham hop, VDC Toan 2022

Câu hỏi: Cho hàm số \(f\left( x \right)\) có đồ thị của hàm số \(y = f'\left( x \right)\) như hình vẽ: Hàm số \(y = f\left( {2x - 1} \right) + \dfrac{{{x^3}}}{3} + {x^2} - 2x\) nghịch biến trên khoảng nào sau đây: A. \(\left( { - 1;0} \right)\) B. \(\left( { - 6; - 3} \right)\) C. \(\left( {3;6} \right)\) D. \(\left( {6; + \infty } \right)\) LỜI GIẢI … [Đọc thêm...] vềHàm số \(y = f\left( {2x – 1} \right) + \dfrac{{{x^3}}}{3} + {x^2} – 2x\) nghịch biến trên khoảng nào sau đây:

Cho hàm số \(f\left( x \right)\) có bảng xét dấu đạo hàm như sau: Hàm số \(y = f\left( {3x + 1} \right) – {x^3} + 3x\) đồng biến trên khoảng nào dưới đây?

Ngày 07/10/2021 Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:Don dieu ham hop, Don dieu VDC

Cho hàm số \(f\left( x \right)\) có bảng xét dấu đạo hàm như sau: Hàm số \(y = f\left( {3x + 1} \right) - {x^3} + 3x\) đồng biến trên khoảng nào dưới đây? A. \(\left( { - 1\,;\, - \frac{1}{3}} \right)\). B. \(\left( {\frac{1}{4}\,;\,\frac{1}{3}} \right)\). C. \(\left( {\frac{2}{3}\,;\,1} \right)\). D. \(\left( {\frac{3}{4}\,;1} \right)\) Lời giải Ta có \(y' = 3f'\left( … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) có bảng xét dấu đạo hàm như sau: Hàm số \(y = f\left( {3x + 1} \right) – {x^3} + 3x\) đồng biến trên khoảng nào dưới đây?