Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 3;8} \right]\) sao cho ứng với mỗi \(m\), hàm số \(y = x - 4\sqrt {x + m} \) nghịch biến trên \(\left( {0;2} \right)\)? A. \(3\) . B. \(6\). C. \(2\). D. \(7\). Lời giải: Điều kiện \(x + m \ge 0,\forall x \in \left( {0;2} \right) \Leftrightarrow m \ge 0\). … [Đọc thêm...] vềCó tất cả bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { – 3;8} \right]\) sao cho ứng với mỗi \(m\), hàm số \(y = x – 4\sqrt {x + m} \) nghịch biến trên \(\left( {0;2} \right)\)?
Don dieu ham hop
nbsp; Cho hàm số \(y = f\left( x \right) = \left( {m + 2} \right){x^4} + \left( {2m – 1} \right){x^2} + 2024\). Số các giá trị nguyên của \(m \in \left[ { – 10;10} \right]\) để hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { – 2;0} \right)\) là
nbsp; Cho hàm số \(y = f\left( x \right) = \left( {m + 2} \right){x^4} + \left( {2m - 1} \right){x^2} + 2024\). Số các giá trị nguyên của \(m \in \left[ { - 10;10} \right]\) để hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { - 2;0} \right)\) là A. \(10\). B. \(9\). C. \(11\). D. \(8\). Lời giải: Chọn … [Đọc thêm...] vềnbsp; Cho hàm số \(y = f\left( x \right) = \left( {m + 2} \right){x^4} + \left( {2m – 1} \right){x^2} + 2024\). Số các giá trị nguyên của \(m \in \left[ { – 10;10} \right]\) để hàm số \(y = f\left( x \right)\) đồng biến trên khoảng \(\left( { – 2;0} \right)\) là
Có bao nhiêu giá trị nguyên của thuộc \(\left[ { – 10;10} \right]\) để hàm số \(y = {\log _2}\left( {3{x^2} – 6\left( {2m + 1} \right)x + 12m + 5} \right)\) đồng biến trên khoảng \(\left( {2;5} \right)\).
Có bao nhiêu giá trị nguyên của thuộc \(\left[ { - 10;10} \right]\) để hàm số \(y = {\log _2}\left( {3{x^2} - 6\left( {2m + 1} \right)x + 12m + 5} \right)\) đồng biến trên khoảng \(\left( {2;5} \right)\). A. 8 B. \(12\). C. \(10\). D. \(11\). Lời giải: Chọn D ĐKXĐ: \(3{x^2} - 6\left( {2m + 1} \right)x + 12m + 5 > 0\) \(y' = \frac{{6x - 6\left( {2m + … [Đọc thêm...] vềCó bao nhiêu giá trị nguyên của thuộc \(\left[ { – 10;10} \right]\) để hàm số \(y = {\log _2}\left( {3{x^2} – 6\left( {2m + 1} \right)x + 12m + 5} \right)\) đồng biến trên khoảng \(\left( {2;5} \right)\).
nbsp; Cho hàm số \(y = {m^2}{x^4} – 2\left( {m + 2024} \right){x^2} + 9\). Có bao nhiêu giá trị nguyên của \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( {1\,;2} \right)\) ?
nbsp; Cho hàm số \(y = {m^2}{x^4} - 2\left( {m + 2024} \right){x^2} + 9\). Có bao nhiêu giá trị nguyên của \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( {1\,;2} \right)\) ? A. \(46\). B. \(45\). C. \(44\). D. \(47\). Lời giải: +) TH1: \(m = 0\) Hàm số đã cho trở thành: \(y = - 4048{x^2} + 9\). Dễ thấy hàm … [Đọc thêm...] vềnbsp; Cho hàm số \(y = {m^2}{x^4} – 2\left( {m + 2024} \right){x^2} + 9\). Có bao nhiêu giá trị nguyên của \(m\) để hàm số đã cho nghịch biến trên khoảng \(\left( {1\,;2} \right)\) ?
Cho hàm số \(y = {\left( {\frac{1}{2}} \right)^{{{\rm{e}}^{2x}} – \,\left( {3m\,\, – \,2} \right){{\rm{e}}^x} + 2024m}}\). Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { – 10;10} \right]\) để hàm số đã cho đồng biến trên khoảng \(\left( {1;2} \right)\)?
Cho hàm số \(y = {\left( {\frac{1}{2}} \right)^{{{\rm{e}}^{2x}} - \,\left( {3m\,\, - \,2} \right){{\rm{e}}^x} + 2024m}}\). Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { - 10;10} \right]\) để hàm số đã cho đồng biến trên khoảng \(\left( {1;2} \right)\)? A. \(6\). B. \(5\). C. \(4\). D. \(7\). Lời giải: Ta có \(y' = {\left( … [Đọc thêm...] vềCho hàm số \(y = {\left( {\frac{1}{2}} \right)^{{{\rm{e}}^{2x}} – \,\left( {3m\,\, – \,2} \right){{\rm{e}}^x} + 2024m}}\). Có bao nhiêu giá trị nguyên của tham số \(m \in \left[ { – 10;10} \right]\) để hàm số đã cho đồng biến trên khoảng \(\left( {1;2} \right)\)?
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị \(\left( C \right)\) của hàm số \(y = {x^4} – 2{m^2}{x^2} + {m^4} + 5\) có ba điểm cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ \(O\) tạo thành một tứ giác nội tiếp. Tìm tích các phần tử của \(S\).
Gọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị \(\left( C \right)\) của hàm số \(y = {x^4} - 2{m^2}{x^2} + {m^4} + 5\) có ba điểm cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ \(O\) tạo thành một tứ giác nội tiếp. Tìm tích các phần tử của \(S\). A. 2. B. \(\frac{1}{5}\). C. \( - \frac{1}{5}\). … [Đọc thêm...] vềGọi \(S\) là tập hợp tất cả các giá trị thực của tham số \(m\) để đồ thị \(\left( C \right)\) của hàm số \(y = {x^4} – 2{m^2}{x^2} + {m^4} + 5\) có ba điểm cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ \(O\) tạo thành một tứ giác nội tiếp. Tìm tích các phần tử của \(S\).
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(R\)và có bảng biến thiên như hình vẽ.
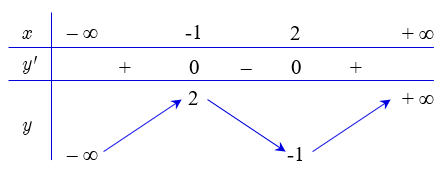
Xét hàm số \(g\left( x \right) = {e^{f\left( {2x + m} \right)}}\). Tìm số giá trị nguyên của tham số \(m \in \left[ { – 2024;2024} \right]\)để hàm số \(g\left( x \right)\)đồng biến trên \(\left( {1;3} \right)\).
Cho hàm số \(y = f\left( x \right)\)liên tục trên \(R\)và có bảng biến thiên như hình vẽ. Xét hàm số \(g\left( x \right) = {e^{f\left( {2x + m} \right)}}\). Tìm số giá trị nguyên của tham số \(m \in \left[ { - 2024;2024} \right]\)để hàm số \(g\left( x \right)\)đồng biến trên \(\left( {1;3} \right)\). A.\(4041\). B. \(2018\). C.\(2025\). … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\)liên tục trên \(R\)và có bảng biến thiên như hình vẽ.
Xét hàm số \(g\left( x \right) = {e^{f\left( {2x + m} \right)}}\). Tìm số giá trị nguyên của tham số \(m \in \left[ { – 2024;2024} \right]\)để hàm số \(g\left( x \right)\)đồng biến trên \(\left( {1;3} \right)\).
Cho hàm số \(y = \frac{{x + m}}{{x – 1}}\) (với \(m\)là thàm số thực) thỏa mãn \(\mathop {\min }\limits_{\left[ {2;5} \right]} y = 3\). Mệnh đề nào sau đây là đúng?
Cho hàm số \(y = \frac{{x + m}}{{x - 1}}\) (với \(m\)là thàm số thực) thỏa mãn \(\mathop {\min }\limits_{\left[ {2;5} \right]} y = 3\). Mệnh đề nào sau đây là đúng? A. \( - 1 < m \le 3\). B. \(4 \le m < 6\). C. \(m > 6\). D. \(m < - 1\). Lời giải: Tập xác định: \(D = \mathbb{R}\backslash \left\{ 1 … [Đọc thêm...] về Cho hàm số \(y = \frac{{x + m}}{{x – 1}}\) (với \(m\)là thàm số thực) thỏa mãn \(\mathop {\min }\limits_{\left[ {2;5} \right]} y = 3\). Mệnh đề nào sau đây là đúng?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
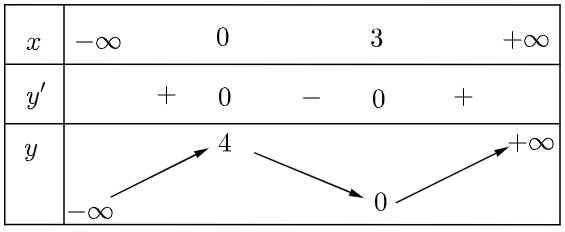
Có bao nhiêu số nguyên dương \(m < 2024\)để hàm số \(g\left( x \right) = f\left( { – {x^2} – 2x + m} \right)\) nghịch biến trên khoảng \(\left( {2;3} \right)\)?
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau Có bao nhiêu số nguyên dương \(m < 2024\)để hàm số \(g\left( x \right) = f\left( { - {x^2} - 2x + m} \right)\) nghịch biến trên khoảng \(\left( {2;3} \right)\)? A. \(2014\). B. \(2015\). C. \(2013\). D. \(2016\). Lời giải: Ta có \(g'\left( x \right) = {\left( … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
Có bao nhiêu số nguyên dương \(m < 2024\)để hàm số \(g\left( x \right) = f\left( { – {x^2} – 2x + m} \right)\) nghịch biến trên khoảng \(\left( {2;3} \right)\)?
Cho hàm số \(y = \frac{{2x + 1}}{{x – 1}}\) có đồ thị \((C)\). Biết \(y = ax + b\) là phương trình tiếp tuyến của \((C)\) có hệ số góc nhỏ nhất trong các tiếp tuyến có hoành độ tiếp điểm là số nguyên dương. Tính \(S = 5a + 4b\).
Cho hàm số \(y = \frac{{2x + 1}}{{x - 1}}\) có đồ thị \((C)\). Biết \(y = ax + b\) là phương trình tiếp tuyến của \((C)\) có hệ số góc nhỏ nhất trong các tiếp tuyến có hoành độ tiếp điểm là số nguyên dương. Tính \(S = 5a + 4b\). A. \( - 29\). B. \(9\). C. \( - 9\). D. \(29\). Lời giải: Ta có \(y' = f'\left( x \right) = \frac{{ … [Đọc thêm...] về Cho hàm số \(y = \frac{{2x + 1}}{{x – 1}}\) có đồ thị \((C)\). Biết \(y = ax + b\) là phương trình tiếp tuyến của \((C)\) có hệ số góc nhỏ nhất trong các tiếp tuyến có hoành độ tiếp điểm là số nguyên dương. Tính \(S = 5a + 4b\).
