Đề bài: Cho $f(x)=x^{2}+3x+4$. Tính $f^{'}(2)$ Lời giải $f^{'}(x)=2x+3$$\Rightarrow f^{'}(2)=7$ … [Đọc thêm...] vềĐề: Cho $f(x)=x^{2}+3x+4$. Tính $f^{'}(2)$
Kết quả tìm kiếm cho: ty so
Đề: Lập bảng xét dấu các biểu thức sau đây:a) \(f(x)=-3x+5\) b)$f(x)=(-2x+4)(x+3)$c) $f(x)=-2+\frac{2x+17}{3x+6}$
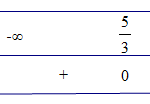
Đề bài: Lập bảng xét dấu các biểu thức sau đây:a) \(f(x)=-3x+5\) b)$f(x)=(-2x+4)(x+3)$c) $f(x)=-2+\frac{2x+17}{3x+6}$ Lời giải Giảia) Ta có: $f(x)=0 \Leftrightarrow -3x+5=0 \Leftrightarrow x=\frac{5}{3}$Bảng xét dấu:b) Ta có: $-2x+4=0 \Leftrightarrow x=2$ và $x+3=0 \Leftrightarrow x=-3$Bảng xét dấu:c) … [Đọc thêm...] vềĐề: Lập bảng xét dấu các biểu thức sau đây:a) \(f(x)=-3x+5\) b)$f(x)=(-2x+4)(x+3)$c) $f(x)=-2+\frac{2x+17}{3x+6}$
Đề: Tìm $m$ để phương trình sau nghiệm đúng với mọi $x$: $ \sin ^mx + \cos ^m x=1$
Đề bài: Tìm $m$ để phương trình sau nghiệm đúng với mọi $x$: $ \sin ^mx + \cos ^m x=1$ Lời giải Đặt $f(x) = \sin ^m x + \cos ^mx $, khi đó yêu cầu bài toán được phát biểu dưới dạng : $ f(x) = 1, \forall x \Leftrightarrow \begin{cases}f'(x) = 0 , \forall x (1) \\ f \left ( \frac{\pi}{4} \right ) =1 (2) \end{cases} $Giải (1) ta được : $m.\cos … [Đọc thêm...] vềĐề: Tìm $m$ để phương trình sau nghiệm đúng với mọi $x$: $ \sin ^mx + \cos ^m x=1$
Đề: Cho đường thẳng $d$ có phương trình $(d):x-2y+15=0$. Tìm trên đường thẳng điểm $M(x_M;y_M)$ sao cho $x_M^2+y_M^2$ nhỏ nhất
Đề bài: Cho đường thẳng $d$ có phương trình $(d):x-2y+15=0$. Tìm trên đường thẳng điểm $M(x_M;y_M)$ sao cho $x_M^2+y_M^2$ nhỏ nhất Lời giải Chuyển phương trình $(d)$ về dạng tham số $(d):\left\{ \begin{array}{l} x=2t-15\\ y=t \end{array} \right. (t\in R)$Điểm $M\in (d)\Rightarrow M(2t-15;t)$Khi đó: $x_M^2+y_M^2=(2t-15)^2+t^2=5t^2-60t+225=5(t-6)^2+45\ge 45$Vậy: $\min … [Đọc thêm...] vềĐề: Cho đường thẳng $d$ có phương trình $(d):x-2y+15=0$. Tìm trên đường thẳng điểm $M(x_M;y_M)$ sao cho $x_M^2+y_M^2$ nhỏ nhất
Đề: a) Cho $x,y.z >0$ và $x+y+z=xyz$. Tìm GTNN $A=x+y+z$b) Cho $x+y=1$. Tìm GTLN $B=x y^{3} $c) Cho $x,y>0,xy=4$ Tìm GTNN $C=x+y+x \sqrt{9+ y^{2}}+y\sqrt{9+x^{2} } $
Đề bài: a) Cho $x,y.z >0$ và $x+y+z=xyz$. Tìm GTNN $A=x+y+z$b) Cho $x+y=1$. Tìm GTLN $B=x y^{3} $c) Cho $x,y>0,xy=4$ Tìm GTNN $C=x+y+x \sqrt{9+ y^{2}}+y\sqrt{9+x^{2} } $ Lời giải Dùng bất đẳng thức cosithêm lời giải chi tiết … [Đọc thêm...] vềĐề: a) Cho $x,y.z >0$ và $x+y+z=xyz$. Tìm GTNN $A=x+y+z$b) Cho $x+y=1$. Tìm GTLN $B=x y^{3} $c) Cho $x,y>0,xy=4$ Tìm GTNN $C=x+y+x \sqrt{9+ y^{2}}+y\sqrt{9+x^{2} } $
Đề: Giải các phương trình :$\begin{array}{l}1)2^x + x – 3 = 0 (1)\\2)3^x + 4^x + 12^x = 13^x (2)\end{array}$
Đề bài: Giải các phương trình :$\begin{array}{l}1)2^x + x - 3 = 0 (1)\\2)3^x + 4^x + 12^x = 13^x (2)\end{array}$ Lời giải $1)$ TXĐ: R.Đặt $f(x) = {2^x} + x - 3$Ta có $f(1) = 0 \Rightarrow x = 1$ là $1$ nghiệm.Cho $x_1>x_2\in R\Rightarrow 2^{x_1}>2^{x_2}\Rightarrow 2^{x_1}+x_1-3>2^{x_2}+x_2-3$$\Rightarrow f(x_1)>f(x_2)$ … [Đọc thêm...] vềĐề: Giải các phương trình :$\begin{array}{l}1)2^x + x – 3 = 0 (1)\\2)3^x + 4^x + 12^x = 13^x (2)\end{array}$
Đề: Cho $y=\sin ^3 x – \cos ^3x.$ Tìm $max y , min y.$
Đề bài: Cho $y=\sin ^3 x - \cos ^3x.$ Tìm $max y , min y.$ Lời giải … [Đọc thêm...] vềĐề: Cho $y=\sin ^3 x – \cos ^3x.$ Tìm $max y , min y.$
Đề: Giải hệ $\begin{cases}\tan x-\tan y=x-y \\ \cos x+\cos y=\sqrt{3} \end{cases} x,y \in (-\frac{\pi}{2};\frac{\pi}{2})$
Đề bài: Giải hệ $\begin{cases}\tan x-\tan y=x-y \\ \cos x+\cos y=\sqrt{3} \end{cases} x,y \in (-\frac{\pi}{2};\frac{\pi}{2})$ Lời giải Xét $f(t)=\tan t-t, t \in (-\frac{\pi}{2};\frac{\pi}{2})$ $f'(t)=\frac{1}{\cos^2 t}-1=\tan^2 t \geq0, \forall t \in (-\frac{\pi}{2};\frac{\pi}{2})$ Dấu $"="$ xảy ra $\Leftrightarrow t=0 \Rightarrow $ $f$ tăng trên … [Đọc thêm...] vềĐề: Giải hệ $\begin{cases}\tan x-\tan y=x-y \\ \cos x+\cos y=\sqrt{3} \end{cases} x,y \in (-\frac{\pi}{2};\frac{\pi}{2})$
Đề: Trong các nghiệm ($x;y$) của bất phương trình:$5{x^2} + 5{y^2} – 5x – 15y + 8 \le 0$Hãy tìm nghiệm có tổng $x + 3y$ nhỏ nhất.
Đề bài: Trong các nghiệm ($x;y$) của bất phương trình:$5{x^2} + 5{y^2} - 5x - 15y + 8 \le 0$Hãy tìm nghiệm có tổng $x + 3y$ nhỏ nhất. Lời giải $5{x^2} + 5{y^2} - 5x - 15y + 8 \le 0 (1)$Đặ $a=x+3y\Rightarrow x=a-3y;$ thay vào $(1)$ ta được:$5(a-3y)^2+5y^2-5(a-3y)-15y+8\leq 0$$\Leftrightarrow 50y^2-30ay+5a^2-5a+8\leq 0 (2)$;$\Delta'=-25a^2+250a-400$Bất phương trình … [Đọc thêm...] vềĐề: Trong các nghiệm ($x;y$) của bất phương trình:$5{x^2} + 5{y^2} – 5x – 15y + 8 \le 0$Hãy tìm nghiệm có tổng $x + 3y$ nhỏ nhất.
Đề: Cho tam thức bậc hai $f(x) = ax^2 +bx+c$. Xác định các giá trị $a,b,c$ biết:a) Tam thức triệt tiêu với $x=\frac{1}{3} $ và $x=-\frac{2}{7} $.b) Tam thức nhận giá trị $3$ khi $x=1$ và $x=-\frac{1}{3} $ và $f(0) =4$.
Đề bài: Cho tam thức bậc hai $f(x) = ax^2 +bx+c$. Xác định các giá trị $a,b,c$ biết:a) Tam thức triệt tiêu với $x=\frac{1}{3} $ và $x=-\frac{2}{7} $.b) Tam thức nhận giá trị $3$ khi $x=1$ và $x=-\frac{1}{3} $ và $f(0) =4$. Lời giải a) Tam thức triệt tiêu với $ x= \frac{1}{3}$ và $x= -\frac{2}{7}$ tức là PT $f(x)=0$ nhận hai giá trị đó làm nghiêm.Theo định lý Vi-ét … [Đọc thêm...] vềĐề: Cho tam thức bậc hai $f(x) = ax^2 +bx+c$. Xác định các giá trị $a,b,c$ biết:a) Tam thức triệt tiêu với $x=\frac{1}{3} $ và $x=-\frac{2}{7} $.b) Tam thức nhận giá trị $3$ khi $x=1$ và $x=-\frac{1}{3} $ và $f(0) =4$.