Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Đề: Tìm:a) GTNN :$f(x,y)=(x-y+1)^{2}+(3x+my+2)^{2}  $b) GTLN,GTNN $C=2x+3y-2z $ với $\begin{cases}2x+y+3z=4 \\ 3x+4y-3z=6\\x,y,z\geq  0 \end{cases} $

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm:a) GTNN :$f(x,y)=(x-y+1)^{2}+(3x+my+2)^{2}  $b) GTLN,GTNN $C=2x+3y-2z $ với $\begin{cases}2x+y+3z=4 \\ 3x+4y-3z=6\\x,y,z\geq  0 \end{cases} $ Lời giải Thêm lời giải chi tiết … [Đọc thêm...] vềĐề: Tìm:a) GTNN :$f(x,y)=(x-y+1)^{2}+(3x+my+2)^{2}  $b) GTLN,GTNN $C=2x+3y-2z $ với $\begin{cases}2x+y+3z=4 \\ 3x+4y-3z=6\\x,y,z\geq  0 \end{cases} $

Đề: $\alpha ,\beta , \gamma $  là 3 góc dương thỏa mãn điều kiện $\alpha  + \beta  + \gamma  = \frac{\pi }{2}$Tìm giá trị lớn nhất của biểu thức:  $g = \sqrt {1 + \tan\alpha \tan\beta }  + \sqrt {1 + \tan\beta \tan\gamma }  + \sqrt {1 + \tan\gamma \tan\alpha } $

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: $\alpha ,\beta , \gamma $  là 3 góc dương thỏa mãn điều kiện $\alpha  + \beta  + \gamma  = \frac{\pi }{2}$Tìm giá trị lớn nhất của biểu thức:  $g = \sqrt {1 + \tan\alpha \tan\beta }  + \sqrt {1 + \tan\beta \tan\gamma }  + \sqrt {1 + \tan\gamma \tan\alpha } $ Lời giải Theo giả thiết ta có: $\pi /2 - \gamma  = \alpha  + \beta $$ \Rightarrow tg(\pi /2 - \gamma ) = … [Đọc thêm...] vềĐề: $\alpha ,\beta , \gamma $  là 3 góc dương thỏa mãn điều kiện $\alpha  + \beta  + \gamma  = \frac{\pi }{2}$Tìm giá trị lớn nhất của biểu thức:  $g = \sqrt {1 + \tan\alpha \tan\beta }  + \sqrt {1 + \tan\beta \tan\gamma }  + \sqrt {1 + \tan\gamma \tan\alpha } $

Đề: Tính diện tích hình phẳng giới hạn bởi  $ (C): y = 4x – x^2$ và các tiếp tuyến với $(C)$ biết rằng các tiếp tuyến này đi qua $A \left ( \frac{5}{2};6 \right )$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tính diện tích hình phẳng giới hạn bởi  $ (C): y = 4x - x^2$ và các tiếp tuyến với $(C)$ biết rằng các tiếp tuyến này đi qua $A \left ( \frac{5}{2};6 \right )$ Lời giải $S = \frac{9}{4}$  (đvdt). … [Đọc thêm...] vềĐề: Tính diện tích hình phẳng giới hạn bởi  $ (C): y = 4x – x^2$ và các tiếp tuyến với $(C)$ biết rằng các tiếp tuyến này đi qua $A \left ( \frac{5}{2};6 \right )$

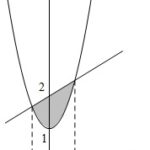
Đề: Cho parabol $y=x^2+1$ và đường thẳng $y = mx +2$.Hãy xác định $m$ để diện tích phẳng giới hạn bởi parabol và đường thẳng là nhỏ nhất.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho parabol $y=x^2+1$ và đường thẳng $y = mx +2$.Hãy xác định $m$ để diện tích phẳng giới hạn bởi parabol và đường thẳng là nhỏ nhất. Lời giải Phương trình hoành độ giao điểm của parabol và đường thẳng:  $ x^2 + 1 = mx + 2 \Leftrightarrow  x^2 - mx -1 =0 \Leftrightarrow  \left[ \begin{array}{l}{x_1} = \frac{{m - \sqrt {{m^2} + 4} }}{2}\\{x_2} = \frac{{m + \sqrt … [Đọc thêm...] vềĐề: Cho parabol $y=x^2+1$ và đường thẳng $y = mx +2$.Hãy xác định $m$ để diện tích phẳng giới hạn bởi parabol và đường thẳng là nhỏ nhất.

Đề:    Cho $x,y,z>1$ thỏa $x+y+z=xyz$. Tìm giá trị nhỏ nhất của:           $P=\frac{y-2}{x^2}+\frac{z-2}{y^2}+\frac{x-2}{z^2}$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài:    Cho $x,y,z>1$ thỏa $x+y+z=xyz$. Tìm giá trị nhỏ nhất của:           $P=\frac{y-2}{x^2}+\frac{z-2}{y^2}+\frac{x-2}{z^2}$ Lời giải                Giải:Theo giả thiết: $\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}=1$Ta có:  $P=\frac{(x-1)+(y-1)}{x^2}+\frac{(y-1)+(z-1)}{y^2}+\frac{(z-1)+(x-z)}{z^2}-(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$    … [Đọc thêm...] vềĐề:    Cho $x,y,z>1$ thỏa $x+y+z=xyz$. Tìm giá trị nhỏ nhất của:           $P=\frac{y-2}{x^2}+\frac{z-2}{y^2}+\frac{x-2}{z^2}$

Đề: Trên mặt phẳng  tọa độ cho điểm $A(3 , 0)$ và parabol $(P)$ có phương trình $y = {x^2}$.a) $M$ là một điểm thuộc parabol $(P)$, có hoành độ ${x_M} = a$. Tính độ dài đoạn $AM$, xác định $a$ để $AM$ ngắn nhất.b) Chứng tỏ rằng nếu đoạn $AM$ ngắn nhất, thì $AM$ vuông góc với tiếp tuyến tại $M$ của parabol $(P)$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Trên mặt phẳng  tọa độ cho điểm $A(3 , 0)$ và parabol $(P)$ có phương trình $y = {x^2}$.a) $M$ là một điểm thuộc parabol $(P)$, có hoành độ ${x_M} = a$. Tính độ dài đoạn $AM$, xác định $a$ để $AM$ ngắn nhất.b) Chứng tỏ rằng nếu đoạn $AM$ ngắn nhất, thì $AM$ vuông góc với tiếp tuyến tại $M$ của parabol $(P)$ Lời giải a) ${x_M} = a \Rightarrow {y_M} = {a^2}$. Do … [Đọc thêm...] vềĐề: Trên mặt phẳng  tọa độ cho điểm $A(3 , 0)$ và parabol $(P)$ có phương trình $y = {x^2}$.a) $M$ là một điểm thuộc parabol $(P)$, có hoành độ ${x_M} = a$. Tính độ dài đoạn $AM$, xác định $a$ để $AM$ ngắn nhất.b) Chứng tỏ rằng nếu đoạn $AM$ ngắn nhất, thì $AM$ vuông góc với tiếp tuyến tại $M$ của parabol $(P)$

Đề: Tìm hai điểm $A,B$ nằm trên đồ thị $(C):y=\frac{x^2}{x-1}$ và đối xứng nhau qua đường thẳng $(d):y=x-1$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm hai điểm $A,B$ nằm trên đồ thị $(C):y=\frac{x^2}{x-1}$ và đối xứng nhau qua đường thẳng $(d):y=x-1$ Lời giải Hai điểm $A,B$ đối xứng nhau qua đường thẳng $(d)$.$\Leftrightarrow AB\bot (d)$ và trung điểm $I$ của $AB$ thuộc $(d)$.*Vì $AB$ vuông góc với $(d)$ nên $(AB):y=-x+m$.Hoành độ giao điểm $A,B$ là nghiệm của phương trình:$\frac{x^{2}}{x-1}=-x+m … [Đọc thêm...] vềĐề: Tìm hai điểm $A,B$ nằm trên đồ thị $(C):y=\frac{x^2}{x-1}$ và đối xứng nhau qua đường thẳng $(d):y=x-1$

Đề: Tìm $a$ sao cho biểu thức:  $ A = \cos 2x – a . \sin ^2 x+ 2 \cos ^2 x $  không phụ thuộc $x$.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm $a$ sao cho biểu thức:  $ A = \cos 2x - a . \sin ^2 x+ 2 \cos ^2 x $  không phụ thuộc $x$. Lời giải Ta có:  $A$ không phụ thuộc $x \Leftrightarrow  A'_x = 0     \forall x $      $ \Leftrightarrow  -2 \sin2x - 2a.\cos x.\sin x-4 \sin x .\cos x = 0   \forall x$      $ \Leftrightarrow  -(a+4)\sin 2x = 0    \forall x \Leftrightarrow  a = -4$Vậy với $a = -4$ thì $A$ … [Đọc thêm...] vềĐề: Tìm $a$ sao cho biểu thức:  $ A = \cos 2x – a . \sin ^2 x+ 2 \cos ^2 x $  không phụ thuộc $x$.

Đề:  Cho họ đường cong  \(y = \frac{{ – {x^2} + mx – {m^2}}}{{x – m}}\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên vẽ đồ thị đường cong khi $m = 1$$2$. Tìm $m$ để đường cong \(\left( {{C_m}} \right)\) có điểm cực đại và cực tiểu$3$. Tìm các điểm trên mặt phẳng tọa độ sao cho có đúng hai đường của họ \(\left( {{C_m}} \right)\) đi qua.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài:  Cho họ đường cong  \(y = \frac{{ - {x^2} + mx - {m^2}}}{{x - m}}\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên vẽ đồ thị đường cong khi $m = 1$$2$. Tìm $m$ để đường cong \(\left( {{C_m}} \right)\) có điểm cực đại và cực tiểu$3$. Tìm các điểm trên mặt phẳng tọa độ sao cho có đúng hai đường của họ \(\left( {{C_m}} \right)\) đi qua. Lời giải $1$. Bạn đọc tự … [Đọc thêm...] vềĐề:  Cho họ đường cong  \(y = \frac{{ – {x^2} + mx – {m^2}}}{{x – m}}\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên vẽ đồ thị đường cong khi $m = 1$$2$. Tìm $m$ để đường cong \(\left( {{C_m}} \right)\) có điểm cực đại và cực tiểu$3$. Tìm các điểm trên mặt phẳng tọa độ sao cho có đúng hai đường của họ \(\left( {{C_m}} \right)\) đi qua.