Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Đề: Tìm tọa độ giao điểm của hai parabol$y = \frac{1}{2} x^2 – x$  và $   y = – 2x^2 + x + \frac{1}{2}$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

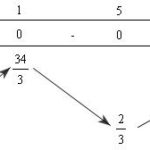
Đề bài: Tìm tọa độ giao điểm của hai parabol$y = \frac{1}{2} x^2 - x$  và $   y = - 2x^2 + x + \frac{1}{2}$ Lời giải Hoành độ giao điểm là nghiệm của phương trình:$\frac{1}{2}x^2 - x = -2x^2 + x + \frac{1}{2}\Leftrightarrow \frac{5}{2}x^2-2x-\frac{1}{2}=0\Leftrightarrow \left[ {\begin{matrix} x=1\\x=-\frac{1}{5} \end{matrix}} \right.$Từ đó, giao điểm là $(1, - … [Đọc thêm...] vềĐề: Tìm tọa độ giao điểm của hai parabol$y = \frac{1}{2} x^2 – x$  và $   y = – 2x^2 + x + \frac{1}{2}$

Đề: Cho $f,g$ liên tục trên $[a,b]$ và $g(x_{0})\neq 0,x_{0}\in [a,b]$Chứng minh rằng:Nếu: $\begin{cases} 0

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho $f,g$ liên tục trên $[a,b]$ và $g(x_{0})\neq 0,x_{0}\in [a,b]$Chứng minh rằng:Nếu: $\begin{cases} 0 Lời giải Đặt: $\begin{cases} \varphi=|g|^{-p},\psi=|fg|^{p}\\ \overline{p}=\frac{1}{p}>1,\overline{q}=\frac{\overline{p}}{\overline{p}-1}=\frac{\frac{1}{p}}{\frac{1}{p}-1}=\frac{1}{1-p}=-\frac{q}{p}>1\end{cases}$Ta chứng minh … [Đọc thêm...] vềĐề: Cho $f,g$ liên tục trên $[a,b]$ và $g(x_{0})\neq 0,x_{0}\in [a,b]$Chứng minh rằng:Nếu: $\begin{cases} 0

Đề: Cho các đường: $y =  – \frac{{{x^3}}}{3} + 3x$        $(P)$  và  $y = m(x – 3)$        $(T)$1) Với giá trị nào của $m$ thì $(T)$ là tiếp tuyến của $(P)$?2) Chứng tỏ họ $(T)$ đi qua một điểm cố định $A$ thuộc $(P)$.3) Gọi $A, B, C$ là các giao điểm của $(P)$ và $(T)$. Hãy tìm m để $OB \bot OC$ ($O$ là gốc tọa độ)

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho các đường: $y =  - \frac{{{x^3}}}{3} + 3x$        $(P)$  và  $y = m(x - 3)$        $(T)$1) Với giá trị nào của $m$ thì $(T)$ là tiếp tuyến của $(P)$?2) Chứng tỏ họ $(T)$ đi qua một điểm cố định $A$ thuộc $(P)$.3) Gọi $A, B, C$ là các giao điểm của $(P)$ và $(T)$. Hãy tìm m để $OB \bot OC$ ($O$ là gốc tọa độ) Lời giải $2)$ Dễ nhận thấy rằng $(T)$ luôn đi qua … [Đọc thêm...] vềĐề: Cho các đường: $y =  – \frac{{{x^3}}}{3} + 3x$        $(P)$  và  $y = m(x – 3)$        $(T)$1) Với giá trị nào của $m$ thì $(T)$ là tiếp tuyến của $(P)$?2) Chứng tỏ họ $(T)$ đi qua một điểm cố định $A$ thuộc $(P)$.3) Gọi $A, B, C$ là các giao điểm của $(P)$ và $(T)$. Hãy tìm m để $OB \bot OC$ ($O$ là gốc tọa độ)

Đề:  Cho họ đường cong  \(y = \frac{{ – {x^2} + mx – {m^2}}}{{x – m}}\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên vẽ đồ thị đường cong khi $m = 1$$2$. Tìm $m$ để đường cong \(\left( {{C_m}} \right)\) có điểm cực đại và cực tiểu$3$. Tìm các điểm trên mặt phẳng tọa độ sao cho có đúng hai đường của họ \(\left( {{C_m}} \right)\) đi qua.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài:  Cho họ đường cong  \(y = \frac{{ - {x^2} + mx - {m^2}}}{{x - m}}\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên vẽ đồ thị đường cong khi $m = 1$$2$. Tìm $m$ để đường cong \(\left( {{C_m}} \right)\) có điểm cực đại và cực tiểu$3$. Tìm các điểm trên mặt phẳng tọa độ sao cho có đúng hai đường của họ \(\left( {{C_m}} \right)\) đi qua. Lời giải $1$. Bạn đọc tự … [Đọc thêm...] vềĐề:  Cho họ đường cong  \(y = \frac{{ – {x^2} + mx – {m^2}}}{{x – m}}\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên vẽ đồ thị đường cong khi $m = 1$$2$. Tìm $m$ để đường cong \(\left( {{C_m}} \right)\) có điểm cực đại và cực tiểu$3$. Tìm các điểm trên mặt phẳng tọa độ sao cho có đúng hai đường của họ \(\left( {{C_m}} \right)\) đi qua.

Đề: Giải hệ bất phương trình: $\left\{ \begin{array}{l}\log _2^2x – {\log _2}x^2 < 0\\\frac{x^3}{3} - 3x^2 + 5x + 9 > 0\end{array} \right.$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Giải hệ bất phương trình: $\left\{ \begin{array}{l}\log _2^2x - {\log _2}x^2 < 0\\\frac{x^3}{3} - 3x^2 + 5x + 9 > 0\end{array} \right.$ Lời giải ĐK :$x>0$$log_2^2x-log_2x^2$\Leftrightarrow  0Xét $f(x)=\frac{x^3}{3} -3x^2+5x+9$ thì $f^/(x)=x^2-6x+5$ $\Rightarrow  f(x)>0 \forall x\in(1,4)$ Do đóHệ $\begin{cases}log_2^2x-log_2x^20 \end{cases} \Leftrightarrow  1 … [Đọc thêm...] vềĐề: Giải hệ bất phương trình: $\left\{ \begin{array}{l}\log _2^2x – {\log _2}x^2 < 0\\\frac{x^3}{3} - 3x^2 + 5x + 9 > 0\end{array} \right.$

Đề: Tìm:a) $GTNN:A=4+a^{2}b^{4}+a^{4}b^{2}-3 a^{2}b^{2} $b) $GTNN: B=x+y$ với $x,y>0$ và $\frac{2}{x}+\frac{3}{y}=6 $

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm:a) $GTNN:A=4+a^{2}b^{4}+a^{4}b^{2}-3 a^{2}b^{2} $b) $GTNN: B=x+y$ với $x,y>0$ và $\frac{2}{x}+\frac{3}{y}=6 $ Lời giải Thêm lời giải chi tiết … [Đọc thêm...] vềĐề: Tìm:a) $GTNN:A=4+a^{2}b^{4}+a^{4}b^{2}-3 a^{2}b^{2} $b) $GTNN: B=x+y$ với $x,y>0$ và $\frac{2}{x}+\frac{3}{y}=6 $

Đề: Cho elip   $(E):   \frac{x^2}{a^2}+\frac{y^2}{b^2}=1  $  với  $F_1(-c;0)$. Tìm  $M$  sao cho  $MF_1$  ngắn nhất.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho elip   $(E):   \frac{x^2}{a^2}+\frac{y^2}{b^2}=1  $  với  $F_1(-c;0)$. Tìm  $M$  sao cho  $MF_1$  ngắn nhất. Lời giải Ta có:   $MF_1=a+ex_M$ Mà   $M \in (E)    \Rightarrow     -a \leq x_M      \Rightarrow      -ea  \leq  ex_M     \Rightarrow    a-ea \leq  a+ex_M=MF_1$Do đó   $MF_1$  ngắn nhất    $\Leftrightarrow  MF_1=a-\frac{c}{a}a=a-c      \Leftrightarrow     … [Đọc thêm...] vềĐề: Cho elip   $(E):   \frac{x^2}{a^2}+\frac{y^2}{b^2}=1  $  với  $F_1(-c;0)$. Tìm  $M$  sao cho  $MF_1$  ngắn nhất.

Đề: Cho $x>0,y>0$ và $xy=4$. Tìm giá trị nhỏ nhất của:a) $P(x;y)=x^2+y^2$.                                          b) $Q(x;y)=(x+1)(4y+3)$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho $x>0,y>0$ và $xy=4$. Tìm giá trị nhỏ nhất của:a) $P(x;y)=x^2+y^2$.                                          b) $Q(x;y)=(x+1)(4y+3)$ Lời giải a) $P(x;y)=x^2+y^2=(x+y)^2-2xy=(x+y)^2-8$Theo hệ quả của bất đẳng thức Côsi cho x và y dương:$(x+y)^2\geq 4xy=16$.  Tích $xy=4$ là hằng số nên tổng $x+y$ nhỏ nhất khi $x=y=2$.Vậy: min $P(x;y)=4^2-8=8$ đạt được khi … [Đọc thêm...] vềĐề: Cho $x>0,y>0$ và $xy=4$. Tìm giá trị nhỏ nhất của:a) $P(x;y)=x^2+y^2$.                                          b) $Q(x;y)=(x+1)(4y+3)$

Đề: Cho $y=\sqrt{\cos ^2 x -2 \cos x +5} + \sqrt{\cos ^2 x – 4 \cos x +8.} $  Tìm $max  y ,  min  y.$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho $y=\sqrt{\cos ^2 x -2 \cos x +5} + \sqrt{\cos ^2 x - 4 \cos x +8.} $  Tìm $max  y ,  min  y.$ Lời giải $y=\sqrt{(1-\cos x)^2+2^2}+\sqrt{(2-\cos x)^2+2^2}\\\le\sqrt{(1+1)^2+2^2}+\sqrt{(2+1)^2+2^2}=2\sqrt2+\sqrt{13}$$y=\sqrt{(1-\cos x)^2+2^2}+\sqrt{(2-\cos x)^2+2^2}\\\ge\sqrt{(1-1)^2+2^2}+\sqrt{(2-1)^2+2^2}=2+\sqrt5$Vậy   $\max  y =2\sqrt2 + \sqrt{13} $  khi  … [Đọc thêm...] vềĐề: Cho $y=\sqrt{\cos ^2 x -2 \cos x +5} + \sqrt{\cos ^2 x – 4 \cos x +8.} $  Tìm $max  y ,  min  y.$

Đề: Chứng minh rằng với $\forall x>0$ luôn có $\ln (x+1)

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Chứng minh rằng với $\forall x>0$ luôn có $\ln (x+1) Lời giải Chúng ta viết lại bất đẳng thức để làm xuất hiện hàm $F$ :    $ \displaystyle \ln (x+1)-00$ nên phép chia không làm đổi dấu)Xét hàm số $F(t)=\ln t$ khả vi và liên tục trên $[1,x+1]$ với $x>0$ theo định lí Lagrange luôn tồn tại $c\in(1,x+1)$ sao cho:   … [Đọc thêm...] vềĐề: Chứng minh rằng với $\forall x>0$ luôn có $\ln (x+1)