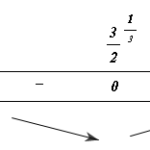
Đề bài: Giải hệ phương trình: $ \left\{ \begin{array}{l}|x - y| + 2|x + y - 1| = 3\\2x + y = 1\end{array} \right.$ Lời giải Từ phương trình thứ 2 $ \Rightarrow y = 1 - 2x $ thay vào phương trình đầu ta có: $ |3x - 1| + 2|x| = 3 $ (3)Xét các khả năng sau :1. Nếu x Nghiệm của hệ là : $ x = - … [Đọc thêm...] vềĐề: Giải hệ phương trình: $ \left\{ \begin{array}{l}|x – y| + 2|x + y – 1| = 3\\2x + y = 1\end{array} \right.$
Kết quả tìm kiếm cho: ty so
Đề: Giải hệ phương trình: $\begin{cases}x^3-3x^2+6x-6=y \\ y^3-3y^2+6y-6=z \\ z^3-3z^2+6z-6=x\end{cases} (I)$
Đề bài: Giải hệ phương trình: $\begin{cases}x^3-3x^2+6x-6=y \\ y^3-3y^2+6y-6=z \\ z^3-3z^2+6z-6=x\end{cases} (I)$ Lời giải Xét hàm số $f(t)=t^3-3t^2+6t-6=(t-1)^3+3t-5$Tập xác định $R$Với mọi $t_1 \in R, t_2 \in R: t_1 $f(t_2)-f(t_1)=[(t_2-1)^3+3t_3-5]-[(t_1-1)^3+3t_1-5]$ =$(t_2-t_1)[(t_2-_1)^2+(t_1-1)^2+(t_2-1)(t_1-1)+3]$ … [Đọc thêm...] vềĐề: Giải hệ phương trình: $\begin{cases}x^3-3x^2+6x-6=y \\ y^3-3y^2+6y-6=z \\ z^3-3z^2+6z-6=x\end{cases} (I)$
Đề: Cho $f(x)=\frac{2x+5}{x-3}$ .Tính $f^{'}(4)$
Đề bài: Cho $f(x)=\frac{2x+5}{x-3}$ .Tính $f^{'}(4)$ Lời giải $f^{'}(x)=\frac{(2x+5)^{'}(x-3)-(2x+5)(x-3)^{'}}{(x-3)^{2}}=\frac{2(x-3)-(2x+5)}{(x-3)^{2}}$ $=-\frac{11}{(x-3)^{2}}$$\Rightarrow f^{'}(4)=-11$ … [Đọc thêm...] vềĐề: Cho $f(x)=\frac{2x+5}{x-3}$ .Tính $f^{'}(4)$
Đề: Cho $f(x)=\sqrt{1+2 \cos x }+\sqrt{1+2 \sin x } . $ Tìm $max f(x) , min f(x). $
Đề bài: Cho $f(x)=\sqrt{1+2 \cos x }+\sqrt{1+2 \sin x } . $ Tìm $max f(x) , min f(x). $ Lời giải Tập xác định của hàm số là $x$ thỏa mãn $\left\{ \begin{array}{l}1 + 2\cos x \ge 0\\1 + 2\sin x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\cos \ge \frac{-1}{2}\\\sin x \ge - \frac{1}{2}\end{array} \right.$$\Leftrightarrow -\frac{ \pi}{6 } … [Đọc thêm...] vềĐề: Cho $f(x)=\sqrt{1+2 \cos x }+\sqrt{1+2 \sin x } . $ Tìm $max f(x) , min f(x). $
Đề: Cho $x,y \geq 0$ và $x+y=1$. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức : $P=3^{2x}+3^y$.
Đề bài: Cho $x,y \geq 0$ và $x+y=1$. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức : $P=3^{2x}+3^y$. Lời giải Ta có: $y=1-x$, từ đó $P=3^{2x} +3^{1-x}=3^{2x}+\frac{1}{3^x}$ với $0 \le x\le1$Đặt $t=3^x$ khi đó $1\le t \le 3$.Xét hàm số $f(t)=t^2+\frac{3}{t}\Rightarrow f'(t)=2t-\frac{3}{t^2}=\frac{2t^3-3}{t^2}$.Từ đó có bảng biến thiên sau:Vậy $\max … [Đọc thêm...] vềĐề: Cho $x,y \geq 0$ và $x+y=1$. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức : $P=3^{2x}+3^y$.
Đề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: $(a_1+a_2+a_3)(a_3+a_4+a_5)(a_5+a_6+a_1)$trong đó $a_1,a_2,a_3,a_4,a_5,a_6$ lấy các giá trị khác nhau trong tập hợp $\{1,2,3,4,5,6\}$
Đề bài: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: $(a_1+a_2+a_3)(a_3+a_4+a_5)(a_5+a_6+a_1)$trong đó $a_1,a_2,a_3,a_4,a_5,a_6$ lấy các giá trị khác nhau trong tập hợp $\{1,2,3,4,5,6\}$ Lời giải Đặt $F=(a_1+a_2+a_3)(a_3+a_4+a_5)(a_5+a_6+a_1)=F(a_1,a_2,a_3,a_4,a_5,a_6)$a. Tìm giá trị lớn nhất của $F$.Áp dụng bất đẳng thức Côsi ta có: $F\leq … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức: $(a_1+a_2+a_3)(a_3+a_4+a_5)(a_5+a_6+a_1)$trong đó $a_1,a_2,a_3,a_4,a_5,a_6$ lấy các giá trị khác nhau trong tập hợp $\{1,2,3,4,5,6\}$
Đề: Cho $f(x)=\frac{x^{2}+x+1}{x+1}$. Tính $f^{'}(1)$
Đề bài: Cho $f(x)=\frac{x^{2}+x+1}{x+1}$. Tính $f^{'}(1)$ Lời giải $f(x)=\frac{(x^{2}+x+1)(x+1)^{'}-(x^{2}+x+1)(x-1)^{'}}{(x-1)^{2}}=\frac{(2x+1)(x+1)-(x^{2}+x+1)}{(x-1)^{2}}$ $=\frac{x^{2}+2x}{(x+1)^{2}}$$\Rightarrow f^{'}(1)=\frac{3}{4}$ … [Đọc thêm...] vềĐề: Cho $f(x)=\frac{x^{2}+x+1}{x+1}$. Tính $f^{'}(1)$
Đề: Cho \(x^{2}+y^{2}=2\) (\(x,y>0\)). Tìm giá trị lớn nhất của \((x+y)xy\).
Đề bài: Cho \(x^{2}+y^{2}=2\) (\(x,y>0\)). Tìm giá trị lớn nhất của \((x+y)xy\). Lời giải Ta có: \(x^{2}+y^{2}\geq 2xy \forall x,y \Rightarrow xy\leq 1\)Theo Bunhiacopski, ta có:\(x+y\leq \sqrt{2(x^{2}+y^{2})} \Rightarrow x+y\leq 2\)Vậy \((x+y)xy\leq 2 \Rightarrow (x+y)xy\) lớn nhất là \(2\) khi \(x=y=1\). … [Đọc thêm...] vềĐề: Cho \(x^{2}+y^{2}=2\) (\(x,y>0\)). Tìm giá trị lớn nhất của \((x+y)xy\).
Đề: Chứng minh rằng:$\frac{1}{1+(n+1)^{2}}
Đề bài: Chứng minh rằng:$\frac{1}{1+(n+1)^{2}} Lời giải Xét $f(x)=\arctan x,x \in [n,n+1]$Theo định lý Lagrange:$\exists c \in (n,n+1)$$f(n+1)-f(n)=f'(c)(n+1-n)$$\Rightarrow \arctan (n+1)-\arctan n=\frac{1}{1+c^{2}}$Mà: $\arctan a-\arctan b=\arctan (\frac{a-b}{1+ab})(1)$$\Rightarrow \arctan \frac{1}{n^{2}+n+1}=\frac{1}{1+c^{2}}$Hơn nữa: $n$\Leftrightarrow … [Đọc thêm...] vềĐề: Chứng minh rằng:$\frac{1}{1+(n+1)^{2}}
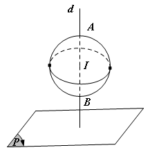
Đề: Tìm điểm $A$ trên mặt cầu $(S): x^2+y^2+z^2-2x+2z-2=0$ sao cho khoảng cách từ $A$ đến mặt phẳng $(P): 2x-2y+z+6=0$ là lớn nhất, nhỏ nhất.
Đề bài: Tìm điểm $A$ trên mặt cầu $(S): x^2+y^2+z^2-2x+2z-2=0$ sao cho khoảng cách từ $A$ đến mặt phẳng $(P): 2x-2y+z+6=0$ là lớn nhất, nhỏ nhất. Lời giải Đưa $(S)$ về dạng: $(x-1)^2+y^2+(z+1)^2=4$.Vậy $(S)$ là mặt cầu tâm tại $I(1;0;-1)$ và bán kính $R=2$.Đường thẳng $(d)$ qua $I$ nhận vectơ pháp tuyến $\overrightarrow{n}=(2;-2;1)$ của $(P)$ là vectơ chỉ phương nên có … [Đọc thêm...] vềĐề: Tìm điểm $A$ trên mặt cầu $(S): x^2+y^2+z^2-2x+2z-2=0$ sao cho khoảng cách từ $A$ đến mặt phẳng $(P): 2x-2y+z+6=0$ là lớn nhất, nhỏ nhất.