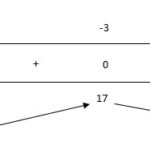
Đề bài: Chứng minh rằng phương trình: $ 5x^4+40x^3+105x^2+100x+24 = 0 $ có bốn nghiệm âm phân biệt. Lời giải Xét hàm số $f(x)=5x^4+40x^3+105x^2+100x+24$$f(x)$ liên tục trên $R$.Ta có: $f(-4)=24, f(-3)=-6, f(-2)=4, f(-1)=-6, f(0)=24$$f(-4).f(-3)=-144$f(-3).f(-2)=-24$f(-2).f(-1)=-24$f(-1).f(0)=-144Các khoảng $(-4;-3); (-3;-2); … [Đọc thêm...] vềĐề: Chứng minh rằng phương trình: $ 5x^4+40x^3+105x^2+100x+24 = 0 $ có bốn nghiệm âm phân biệt.
Kết quả tìm kiếm cho: ty so
Đề: Tìm giá trị lớn nhất của biểu thức:$A=\sqrt{a+\cos x}+\sqrt{a+\sin x}$ với $x\in R,a\geq 1$
Đề bài: Tìm giá trị lớn nhất của biểu thức:$A=\sqrt{a+\cos x}+\sqrt{a+\sin x}$ với $x\in R,a\geq 1$ Lời giải Trong mặt phẳng tọa độ $Oxy$ chọn:$\overrightarrow {u}=(1;1) \Rightarrow |\overrightarrow {u}|=\sqrt{2}$$\overrightarrow {v}=(\sqrt{a+\cos x};\sqrt{a+\sin x}) \Rightarrow |\overrightarrow {v}|=\sqrt{2a+\sqrt{2}\sin (x+\frac{\pi}{4})}$$A=\overrightarrow … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất của biểu thức:$A=\sqrt{a+\cos x}+\sqrt{a+\sin x}$ với $x\in R,a\geq 1$
Đề: Chứng minh rằng phương trình $4x^{4}+2x^{2}-x-3=0$ có ít nhất hai nghiệm phân biệt trên khoảng $(-1,1)$
Đề bài: Chứng minh rằng phương trình $4x^{4}+2x^{2}-x-3=0$ có ít nhất hai nghiệm phân biệt trên khoảng $(-1,1)$ Lời giải Xét hàm số $f(x)=4x^{4}+2x^{2}-x-3$Vì $f(x)$ là hàm đa thức nên liên tục trên các đoạn $[-1,0]$ và $[0,1]$Ngoài ra $\begin{cases}f(-1)=4 \\ f(0)=-3 \end{cases}$$\Rightarrow f(-1).f(0)=-12nên phương trình $f(x)=0$ có ít nhất một nghiệm $x_{1}\in (-1,0)$và … [Đọc thêm...] vềĐề: Chứng minh rằng phương trình $4x^{4}+2x^{2}-x-3=0$ có ít nhất hai nghiệm phân biệt trên khoảng $(-1,1)$
Đề: Chứng minh rằng : $\forall x \in \left( {0,\frac{\pi }{2}} \right)$ ta có ${2^{2\sin x}} + {2^{tanx}} > {2^{\frac{{3x}}{2} + 1}}$
Đề bài: Chứng minh rằng : $\forall x \in \left( {0,\frac{\pi }{2}} \right)$ ta có ${2^{2\sin x}} + {2^{tanx}} > {2^{\frac{{3x}}{2} + 1}}$ Lời giải Áp dụng bất đẳng thức côsi:${2^{2\sin x}} + {2^{tanx}} \ge 2\sqrt {{2^{2\sin x + tanx}}} = {2.2^{\frac{{2\sin x + tanx}}{2}}}$Ta có ${2^{\frac{{3x}}{2} + 1}} = {2.2^{\frac{{3x}}{2}}} $. So sánh $2\sin x + tanx $ với $3x$ trên … [Đọc thêm...] vềĐề: Chứng minh rằng : $\forall x \in \left( {0,\frac{\pi }{2}} \right)$ ta có ${2^{2\sin x}} + {2^{tanx}} > {2^{\frac{{3x}}{2} + 1}}$
Đề: Cho biểu thức $P$ = \(\cos A + \cos B + \cos C\). Trong đó $A, B, C$ là các góc của tam giác $ABC$ bất kì. Chứng minh rằng $P$ đạt giá trị lớn nhất nhưng không đạt giá trị nhỏ nhất.
Đề bài: Cho biểu thức $P$ = \(\cos A + \cos B + \cos C\). Trong đó $A, B, C$ là các góc của tam giác $ABC$ bất kì. Chứng minh rằng $P$ đạt giá trị lớn nhất nhưng không đạt giá trị nhỏ nhất. Lời giải $P=$ \(\cos A + \cos B + \cos C = 2\cos \frac{{A + B}}{2}c{\rm{os}}\frac{{A - B}}{2} + 1 - 2{\sin ^2}\frac{C}{2}\) \(= 1 + 2\sin \frac{C}{2}c{\rm{os}}\frac{{A - B}}{2} + 1 - … [Đọc thêm...] vềĐề: Cho biểu thức $P$ = \(\cos A + \cos B + \cos C\). Trong đó $A, B, C$ là các góc của tam giác $ABC$ bất kì. Chứng minh rằng $P$ đạt giá trị lớn nhất nhưng không đạt giá trị nhỏ nhất.
Đề: Chứng minh rằng phương trình $x^{3}+3x^{2}+5x-1=0$ có ít nhất một nghiệm trên khoảng $(0,1)$
Đề bài: Chứng minh rằng phương trình $x^{3}+3x^{2}+5x-1=0$ có ít nhất một nghiệm trên khoảng $(0,1)$ Lời giải Xét hàm số $f(x)=x^{3}+3x^{2}+5x-1$$f(x)$ là hàm đa thức nên liên tục trên đoạn $[0,1]$Mặt khác: $\begin{cases}f(0)=-1 \\ f(1)=8 \end{cases}$$\Rightarrow f(0).f(1)=-8Vậy phương trình $f(x)=0$ có ít nhất một nghiệm trên khoảng $(0,1)$ … [Đọc thêm...] vềĐề: Chứng minh rằng phương trình $x^{3}+3x^{2}+5x-1=0$ có ít nhất một nghiệm trên khoảng $(0,1)$
Đề: Cho $f(x)=\sqrt{1+2 \cos x }+\sqrt{1+2 \sin x } . $ Tìm $max f(x) , min f(x). $
Đề bài: Cho $f(x)=\sqrt{1+2 \cos x }+\sqrt{1+2 \sin x } . $ Tìm $max f(x) , min f(x). $ Lời giải Tập xác định của hàm số là $x$ thỏa mãn $\left\{ \begin{array}{l}1 + 2\cos x \ge 0\\1 + 2\sin x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\cos \ge \frac{-1}{2}\\\sin x \ge - \frac{1}{2}\end{array} \right.$$\Leftrightarrow -\frac{ \pi}{6 } … [Đọc thêm...] vềĐề: Cho $f(x)=\sqrt{1+2 \cos x }+\sqrt{1+2 \sin x } . $ Tìm $max f(x) , min f(x). $
Đề: Bỏ dấu trị tuyệt đối trong biểu thức của \(f(x)\)a) \(f(x)=|-3x+2|\) b) $ f(x)=|2x+5||3-4x|$
Đề bài: Bỏ dấu trị tuyệt đối trong biểu thức của \(f(x)\)a) \(f(x)=|-3x+2|\) b) $ f(x)=|2x+5||3-4x|$ Lời giải Cần giải chi tiết … [Đọc thêm...] vềĐề: Bỏ dấu trị tuyệt đối trong biểu thức của \(f(x)\)a) \(f(x)=|-3x+2|\) b) $ f(x)=|2x+5||3-4x|$
Đề: Xét dấu của biểu thức sau: $g(x)=\frac{x^2-5x+4}{x^2-x-6}$
Đề bài: Xét dấu của biểu thức sau: $g(x)=\frac{x^2-5x+4}{x^2-x-6}$ Lời giải Giải Xét tam thức $x^2-5x+4 có \Delta_1=(-5)^2-4.1.4=9>0$Tam thức $x^2-5x+4$ có hai nghiệm là $x_1=1, x_2=4$ Tương tự $\Delta_2=(-1)^2-4.(-6)=25$Tam thức $x^2-x-6$ có hai nghiệm là $x_3=\frac{1-5}{2}=-2, x_4=\frac{1+5}{2}=3$.Ta lập bảng sau:Kết luận $g(x)>0, \forall x\in (-\infty ;-2)\cup … [Đọc thêm...] vềĐề: Xét dấu của biểu thức sau: $g(x)=\frac{x^2-5x+4}{x^2-x-6}$
Đề: Giải hệ bất phương trình: $\left\{ \begin{array}{l}{x^2} + 5x + 4 < 0\\{x^3} + 3{x^2} - 9x - 10 > 0\end{array} \right.$
Đề bài: Giải hệ bất phương trình: $\left\{ \begin{array}{l}{x^2} + 5x + 4 < 0\\{x^3} + 3{x^2} - 9x - 10 > 0\end{array} \right.$ Lời giải Giải hệ : $\left\{ \begin{array}{l}{x^2} + 5x + 4 {x^3} + 3{x^2} - 9x - 10 > 0\end{array} \right.\Leftrightarrow \begin{cases}-40 \end{cases} $Xét hàm $f(x)=x^3+3x^2-9x-10, x\in (-4;-1)$$f'(x)=3x^2+6x-9, f'(x)=0\Leftrightarrow x=-3, … [Đọc thêm...] vềĐề: Giải hệ bất phương trình: $\left\{ \begin{array}{l}{x^2} + 5x + 4 < 0\\{x^3} + 3{x^2} - 9x - 10 > 0\end{array} \right.$