100. Đề thi thử TN THPT môn Toán năm 2024 - THPT-ĐẶNG-THÚC-HỨA-L2-23-24_.docx ========== booktoan.com chia sẻ đến các ĐỀ THI TN THPT MÔN TOÁN 2024. Đề THI có đáp án chi tiết giúp các em đối chiếu, tham khảo để đánh giá năng lực bản thân. Chúc các em thành công và đạt kết quả cao trong kỳ thi TN THPT năm nay, ĐỖ NGUYỆN VỌNG 1. NGUỒN: BOOKTOAN.COM sưu tập trên … [Đọc thêm...] về100. Đề thi thử TN THPT môn Toán năm 2024 – THPT-ĐẶNG-THÚC-HỨA-L2-23-24_.docx
Kết quả tìm kiếm cho: 0a
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} + x – 6\) với mọi \(x \in \mathbb{R}\). Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} – 9x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0;4} \right)\). Tính tổng các phần tử của \(S\).
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2} + x - 6\) với mọi \(x \in \mathbb{R}\). Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} - 3{x^2} - 9x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0;4} \right)\). Tính tổng các phần tử của … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} + x – 6\) với mọi \(x \in \mathbb{R}\). Gọi \(S\) là tập hợp các giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} – 9x + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( {0;4} \right)\). Tính tổng các phần tử của \(S\).
Cho đường tròn \(\left( C \right)\) và \(\left( {C’} \right)\) có cùng bán kính \(R = 3\) thỏa mãn tính chất tâm \(O\) của \(\left( C \right)\)thuộc \(\left( {C’} \right)\)và ngược lại tâm \(O’\) của \(\left( {C’} \right)\)thuộc \(\left( C \right)\). Khi hai đường tròn \(\left( C \right)\) và \(\left( {C’} \right)\) quay quanh đường \(OO’\)tạo ra hai mặt cầu \(\left( S \right),\,\left( {S’} \right)\) Tính thể tích \(V\) phần chung của hai khối cầu tạo bởi \(\left( S \right),\,\left( {S’} \right)\)là
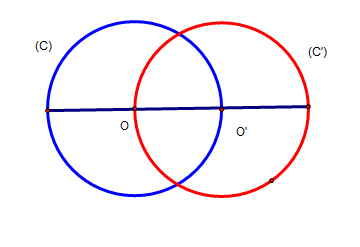
Cho đường tròn \(\left( C \right)\) và \(\left( {C'} \right)\) có cùng bán kính \(R = 3\) thỏa mãn tính chất tâm \(O\) của \(\left( C \right)\)thuộc \(\left( {C'} \right)\)và ngược lại tâm \(O'\) của \(\left( {C'} \right)\)thuộc \(\left( C \right)\). Khi hai đường tròn \(\left( C \right)\) và \(\left( {C'} \right)\) quay quanh đường \(OO'\)tạo ra hai mặt cầu \(\left( S … [Đọc thêm...] vềCho đường tròn \(\left( C \right)\) và \(\left( {C’} \right)\) có cùng bán kính \(R = 3\) thỏa mãn tính chất tâm \(O\) của \(\left( C \right)\)thuộc \(\left( {C’} \right)\)và ngược lại tâm \(O’\) của \(\left( {C’} \right)\)thuộc \(\left( C \right)\). Khi hai đường tròn \(\left( C \right)\) và \(\left( {C’} \right)\) quay quanh đường \(OO’\)tạo ra hai mặt cầu \(\left( S \right),\,\left( {S’} \right)\) Tính thể tích \(V\) phần chung của hai khối cầu tạo bởi \(\left( S \right),\,\left( {S’} \right)\)là
Trong mặt phẳng tọa độ \(Oxy\), cho hình vuông \(OABC\), với \(A\left( {4;0} \right),\,B\left( {4;4} \right),\,C\left( {0;4} \right)\). Một đồ thị \(\left( C \right)\) của hàm số bậc ba\(y = a{x^3} + b{x^2} + cx + d\), với \(a \ne 0\) đi qua hai điểm \(O\) và \(B\), đồng thời tiếp xúc với hai đường thẳng \(OA\), \(BC\); chia hình vuông \(OABC\) thành 4 phần (như hình vẽ). Gọi \({S_1},\,{S_2}\) lần lượt là diện tích của 2 miền chấm bi, gạch chéo như hình vẽ.
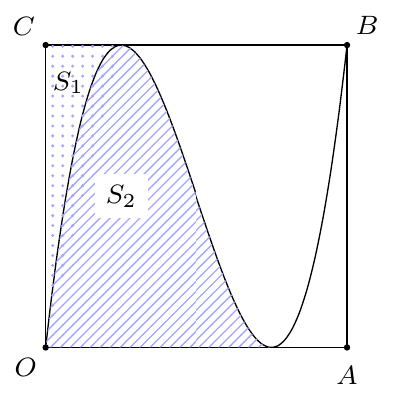
Đặt \(k = \frac{{{S_2}}}{{{S_1}}}\) và \(T = 2025k – 2024\). Khẳng định nào sau đây là đúng?
Trong mặt phẳng tọa độ \(Oxy\), cho hình vuông \(OABC\), với \(A\left( {4;0} \right),\,B\left( {4;4} \right),\,C\left( {0;4} \right)\). Một đồ thị \(\left( C \right)\) của hàm số bậc ba\(y = a{x^3} + b{x^2} + cx + d\), với \(a \ne 0\) đi qua hai điểm \(O\) và \(B\), đồng thời tiếp xúc với hai đường thẳng \(OA\), \(BC\); chia hình vuông \(OABC\) thành 4 phần (như hình vẽ). Gọi … [Đọc thêm...] vềTrong mặt phẳng tọa độ \(Oxy\), cho hình vuông \(OABC\), với \(A\left( {4;0} \right),\,B\left( {4;4} \right),\,C\left( {0;4} \right)\). Một đồ thị \(\left( C \right)\) của hàm số bậc ba\(y = a{x^3} + b{x^2} + cx + d\), với \(a \ne 0\) đi qua hai điểm \(O\) và \(B\), đồng thời tiếp xúc với hai đường thẳng \(OA\), \(BC\); chia hình vuông \(OABC\) thành 4 phần (như hình vẽ). Gọi \({S_1},\,{S_2}\) lần lượt là diện tích của 2 miền chấm bi, gạch chéo như hình vẽ.
Đặt \(k = \frac{{{S_2}}}{{{S_1}}}\) và \(T = 2025k – 2024\). Khẳng định nào sau đây là đúng?
Săm lốp xe ô tô khi bơm căng đặt nằm trên mặt phẳng nằm ngang có hình chiếu bằng như hình vẽ với bán kính đường tròn nhỏ \({R_1} = 20cm\), bán kính đường tròn lớn \({R_2} = 30cm\) và mặt cắt khi cắt bởi mặt phẳng đi qua trục, vuông góc mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày vỏ săm. Tính thể tích không khí được chứa bên trong săm.

Săm lốp xe ô tô khi bơm căng đặt nằm trên mặt phẳng nằm ngang có hình chiếu bằng như hình vẽ với bán kính đường tròn nhỏ \({R_1} = 20cm\), bán kính đường tròn lớn \({R_2} = 30cm\) và mặt cắt khi cắt bởi mặt phẳng đi qua trục, vuông góc mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày vỏ săm. Tính thể tích không khí được chứa bên trong săm. A. \(1250{\pi … [Đọc thêm...] vềSăm lốp xe ô tô khi bơm căng đặt nằm trên mặt phẳng nằm ngang có hình chiếu bằng như hình vẽ với bán kính đường tròn nhỏ \({R_1} = 20cm\), bán kính đường tròn lớn \({R_2} = 30cm\) và mặt cắt khi cắt bởi mặt phẳng đi qua trục, vuông góc mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày vỏ săm. Tính thể tích không khí được chứa bên trong săm.
Xét các số thực dương \(x,{\rm{ }}y\) thỏa mãn \({\log _{\sqrt 3 }}\frac{{x + y}}{{{x^2} + {y^2} + xy + 2}} = x\left( {x – 3} \right) + y\left( {y – 3} \right) + xy\).
Tìm giá trị lớn nhất của \(P = \frac{{3x + 2y + 1}}{{x + y + 6}}\).
Xét các số thực dương \(x,{\rm{ }}y\) thỏa mãn \({\log _{\sqrt 3 }}\frac{{x + y}}{{{x^2} + {y^2} + xy + 2}} = x\left( {x - 3} \right) + y\left( {y - 3} \right) + xy\). Tìm giá trị lớn nhất của \(P = \frac{{3x + 2y + 1}}{{x + y + 6}}\). A. \(3\) B. \(4\) C. \(2\) D. \(1\) Lời giải: Chọn D Ta có \({\log _{\sqrt 3 }}\frac{{x + y}}{{{x^2} + {y^2} + xy + 2}} … [Đọc thêm...] vềXét các số thực dương \(x,{\rm{ }}y\) thỏa mãn \({\log _{\sqrt 3 }}\frac{{x + y}}{{{x^2} + {y^2} + xy + 2}} = x\left( {x – 3} \right) + y\left( {y – 3} \right) + xy\).
Tìm giá trị lớn nhất của \(P = \frac{{3x + 2y + 1}}{{x + y + 6}}\).
Trong không gian cho tam giác\(ABC\) vuông tại \(A\),\(AB = a\) và \(\widehat {ACB} = {30^o}\). Tính thể tích \(V\) của khối nón nhận được khi quay tam giác \(ABC\) quanh cạnh \(AC\).
Trong không gian cho tam giác\(ABC\) vuông tại \(A\),\(AB = a\) và \(\widehat {ACB} = {30^o}\). Tính thể tích \(V\) của khối nón nhận được khi quay tam giác \(ABC\) quanh cạnh \(AC\). A. \(V = \pi {a^3}\). B. \(V = \sqrt 3 \pi {a^3}\). C.\(V = \frac{{\sqrt 3 \pi {a^3}}}{9}\) . D. \(V = \frac{{\sqrt 3 \pi {a^3}}}{3}\). Lời giải: Ta có \(AC = AB.\cot {30^o} = … [Đọc thêm...] vềTrong không gian cho tam giác\(ABC\) vuông tại \(A\),\(AB = a\) và \(\widehat {ACB} = {30^o}\). Tính thể tích \(V\) của khối nón nhận được khi quay tam giác \(ABC\) quanh cạnh \(AC\).
Cho hình thang \(ABCD\) có \(\widehat A = \widehat B = 90^\circ \), \(AB = BC = a\), \(AD = 2a\). Tính thể tích khối tròn xoay sinh ra khi quay hình thang \(ABCD\) xung quanh trục \(CD\).

Cho hình thang \(ABCD\) có \(\widehat A = \widehat B = 90^\circ \), \(AB = BC = a\), \(AD = 2a\). Tính thể tích khối tròn xoay sinh ra khi quay hình thang \(ABCD\) xung quanh trục \(CD\). A. \(\frac{{7\sqrt 2 \,\pi {a^3}}}{6}\) B. \(\frac{{7\sqrt 2 \pi {a^3}}}{{12}}\) C. \(\frac{{7\pi {a^3}}}{6}\) D. \(\frac{{7\pi {a^3}}}{{12}}\) Lời giải: Gọi \(E\) là … [Đọc thêm...] vềCho hình thang \(ABCD\) có \(\widehat A = \widehat B = 90^\circ \), \(AB = BC = a\), \(AD = 2a\). Tính thể tích khối tròn xoay sinh ra khi quay hình thang \(ABCD\) xung quanh trục \(CD\).
Trong không gian \(Oxyz\),cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} – 2x + 2z – 2 = 0\) và các điểm \(A\left( {0\,;1;\,1} \right)\), \(B\left( { – 1; – 2; – 3} \right)\),\(C\left( {1;0; – 3} \right)\). Điểm \(D\) thuộc mặt cầu \(\left( S \right)\). Thể tích tứ diện \(ABCD\) lớn nhất bằng
Trong không gian \(Oxyz\),cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x + 2z - 2 = 0\) và các điểm \(A\left( {0\,;1;\,1} \right)\), \(B\left( { - 1; - 2; - 3} \right)\),\(C\left( {1;0; - 3} \right)\). Điểm \(D\) thuộc mặt cầu \(\left( S \right)\). Thể tích tứ diện \(ABCD\) lớn nhất bằng A. \(\frac{{16}}{3}\). B. \(9\). C. \(\frac{8}{3}\). D. … [Đọc thêm...] vềTrong không gian \(Oxyz\),cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} – 2x + 2z – 2 = 0\) và các điểm \(A\left( {0\,;1;\,1} \right)\), \(B\left( { – 1; – 2; – 3} \right)\),\(C\left( {1;0; – 3} \right)\). Điểm \(D\) thuộc mặt cầu \(\left( S \right)\). Thể tích tứ diện \(ABCD\) lớn nhất bằng
Trong không gian với hệ trục toạ độ \(Oxyz\), cho đường thẳng \(d:\,\frac{{x – 2}}{2} = \frac{y}{{ – 1}} = \frac{z}{4}\) và mặt cầu \(\left( S \right)\,:{\,^{}}{\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 1} \right)^2} = 2\) có tâm là \(I\). Hai mặt phẳng \(\left( P \right),\left( Q \right)\) chứa \(d\) và tiếp xúc với \(\left( S \right)\) tại hai tiếp điểm \(A,B\). Tìm toạ độ điểm \(D\) thuộc đường thẳng \(d\) sao cho thể tích khối chóp \(
D.AIB\) bằng \(\sqrt {42} \).
Trong không gian với hệ trục toạ độ \(Oxyz\), cho đường thẳng \(d:\,\frac{{x - 2}}{2} = \frac{y}{{ - 1}} = \frac{z}{4}\) và mặt cầu \(\left( S \right)\,:{\,^{}}{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 1} \right)^2} = 2\) có tâm là \(I\). Hai mặt phẳng \(\left( P \right),\left( Q \right)\) chứa \(d\) và tiếp xúc với \(\left( S \right)\) tại hai tiếp … [Đọc thêm...] vềTrong không gian với hệ trục toạ độ \(Oxyz\), cho đường thẳng \(d:\,\frac{{x – 2}}{2} = \frac{y}{{ – 1}} = \frac{z}{4}\) và mặt cầu \(\left( S \right)\,:{\,^{}}{\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 1} \right)^2} = 2\) có tâm là \(I\). Hai mặt phẳng \(\left( P \right),\left( Q \right)\) chứa \(d\) và tiếp xúc với \(\left( S \right)\) tại hai tiếp điểm \(A,B\). Tìm toạ độ điểm \(D\) thuộc đường thẳng \(d\) sao cho thể tích khối chóp \(
D.AIB\) bằng \(\sqrt {42} \).
