Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: 0a

Cho tích phân \(I = \int\limits_0^\pi {\frac{{x\sin x}}{{{{\cos }^2}x – 16}}} dx = a\pi \ln \frac{b}{c},\,\left( {a,b,c \in \mathbb{Q},0 < b < c < 8} \right)\). Giá trị của biểu thức \(40a + 3b – {c^2}\)là

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:,

Cho tích phân \(I = \int\limits_0^\pi {\frac{{x\sin x}}{{{{\cos }^2}x - 16}}} dx = a\pi \ln \frac{b}{c},\,\left( {a,b,c \in \mathbb{Q},0 < b < c < 8} \right)\). Giá trị của biểu thức \(40a + 3b - {c^2}\)là A.\(17\). B.\(13\). C.\( - 9\). D.\( - 11\). Lời giải: Đặt \(t = \pi - x \Leftrightarrow x = \pi - t \Rightarrow dx = - dt\). Đổi cận \(\left\{ … [Đọc thêm...] vềCho tích phân \(I = \int\limits_0^\pi {\frac{{x\sin x}}{{{{\cos }^2}x – 16}}} dx = a\pi \ln \frac{b}{c},\,\left( {a,b,c \in \mathbb{Q},0 < b < c < 8} \right)\). Giá trị của biểu thức \(40a + 3b – {c^2}\)là

Một bàn dài có 2 dãy ghế đối diện nhau, mỗi dãy gồm 6 ghế. Lớp 10A có 12 học sinh gồm 6 nam và 6 nữ. Hỏi có bao nhiêu cách xếp 12 học sinh đó vào 2 dãy ghế sao cho các học sinh khác giới ngồi đối diện nhau?

Ngày Thuộc chủ đề:Trắc nghiệm Tổ hợp Tag với:

Một bàn dài có 2 dãy ghế đối diện nhau, mỗi dãy gồm 6 ghế. Lớp 10A có 12 học sinh gồm 6 nam và 6 nữ. Hỏi có bao nhiêu cách xếp 12 học sinh đó vào 2 dãy ghế sao cho các học sinh khác giới ngồi đối diện nhau? A. \(33177600\).           B .   \(518400\).            C .   \(1036800\).         D .   \(16588800\). Lời giải Chọn A Mô tả 2 dãy … [Đọc thêm...] vềMột bàn dài có 2 dãy ghế đối diện nhau, mỗi dãy gồm 6 ghế. Lớp 10A có 12 học sinh gồm 6 nam và 6 nữ. Hỏi có bao nhiêu cách xếp 12 học sinh đó vào 2 dãy ghế sao cho các học sinh khác giới ngồi đối diện nhau?

Đề toán 2022 [Mức độ 3] Cho hàm số bậc bốn \(y = f\left( x \right)\). Biết rằng hàm số \(g\left( x \right) = \ln f\left( x \right)\) có bảng biến thiên như sau:

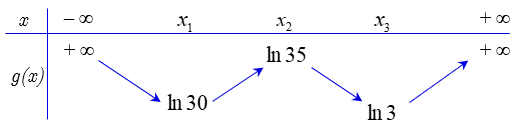
Chart Description automatically generated

Diện tích hình phẳng giới hạn bởi các đường \(y = f’\left( x \right)\) và \(y = g’\left( x \right)\) thuộc khoảng nào dưới đây?

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:,

Đề toán 2022 [Mức độ 3] Cho hàm số bậc bốn \(y = f\left( x \right)\). Biết rằng hàm số \(g\left( x \right) = \ln f\left( x \right)\) có bảng biến thiên như sau: Diện tích hình phẳng giới hạn bởi các đường \(y = f'\left( x \right)\) và \(y = g'\left( x \right)\) thuộc khoảng nào dưới đây? A. \(\left( {33;35} \right)\). B. \(\left( {37;40} \right)\). C. \(\left( {29;32} … [Đọc thêm...] về

Đề toán 2022 [Mức độ 3] Cho hàm số bậc bốn \(y = f\left( x \right)\). Biết rằng hàm số \(g\left( x \right) = \ln f\left( x \right)\) có bảng biến thiên như sau:

Chart Description automatically generated

Diện tích hình phẳng giới hạn bởi các đường \(y = f’\left( x \right)\) và \(y = g’\left( x \right)\) thuộc khoảng nào dưới đây?

Một chiếc tạ tay có hình dạng gồm 3 khối trụ, trong đó hai khối trụ ở hai đầu bằng nhau và khối trụ làm tay cầm ở giữa. Gọi khối trụ làm đầu tạ là \(\left( {{T_1}} \right)\) và khối trụ làm tay cầm là \(\left( {{T_2}} \right)\)lần lượt có bán kính và chiều cao tương ứng là \({r_1}\), \({h_1}\), \({r_2}\), \({h_2}\) thỏa mãn \({r_1} = 4{r_2}\), \({h_1} = \frac{1}{2}{h_2}\).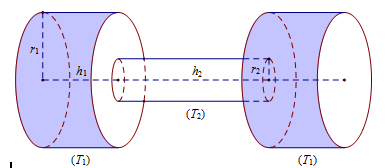Biết rằng thể tích của khối trụ tay cầm \(\left( {{T_2}} \right)\) bằng 30 \(\left( {c{m^3}} \right)\) và chiếc tạ làm bằng inox có khối lượng riêng là \(D = 7,7g/c{m^3}\). Khối lượng của chiếc tạ tay bằng

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

Câu hỏi: Một chiếc tạ tay có hình dạng gồm 3 khối trụ, trong đó hai khối trụ ở hai đầu bằng nhau và khối trụ làm tay cầm ở giữa. Gọi khối trụ làm đầu tạ là \(\left( {{T_1}} \right)\) và khối trụ làm tay cầm là \(\left( {{T_2}} \right)\)lần lượt có bán kính và chiều cao tương ứng là \({r_1}\), \({h_1}\), \({r_2}\), \({h_2}\) thỏa mãn \({r_1} = 4{r_2}\), \({h_1} = … [Đọc thêm...] vềMột chiếc tạ tay có hình dạng gồm 3 khối trụ, trong đó hai khối trụ ở hai đầu bằng nhau và khối trụ làm tay cầm ở giữa. Gọi khối trụ làm đầu tạ là \(\left( {{T_1}} \right)\) và khối trụ làm tay cầm là \(\left( {{T_2}} \right)\)lần lượt có bán kính và chiều cao tương ứng là \({r_1}\), \({h_1}\), \({r_2}\), \({h_2}\) thỏa mãn \({r_1} = 4{r_2}\), \({h_1} = \frac{1}{2}{h_2}\).Biết rằng thể tích của khối trụ tay cầm \(\left( {{T_2}} \right)\) bằng 30 \(\left( {c{m^3}} \right)\) và chiếc tạ làm bằng inox có khối lượng riêng là \(D = 7,7g/c{m^3}\). Khối lượng của chiếc tạ tay bằng

Que kem ốc quế có lượng kem gồm: phần kem trong phần ốc quế có dạng hình nón và phần kem nhô ra phía trên có dạng nửa khối cầu. Biết hình nón có chiều cao \(h = 10\,cm\), còn bán kính khối cầu bằng bán kính đường tròn đáy r của hình nón, biết \(r = 3\,cm\). Tính gần đúng lượng kem cần để làm được \(100\) que kem ốc quế.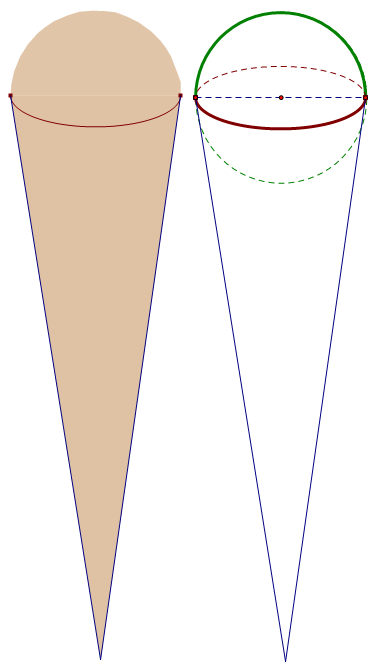

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

Câu hỏi: Que kem ốc quế có lượng kem gồm: phần kem trong phần ốc quế có dạng hình nón và phần kem nhô ra phía trên có dạng nửa khối cầu. Biết hình nón có chiều cao \(h = 10\,cm\), còn bán kính khối cầu bằng bán kính đường tròn đáy r của hình nón, biết \(r = 3\,cm\). Tính gần đúng lượng kem cần để làm được \(100\) que kem ốc quế. A.\(12252,21\,c{m^3}\). B. … [Đọc thêm...] vềQue kem ốc quế có lượng kem gồm: phần kem trong phần ốc quế có dạng hình nón và phần kem nhô ra phía trên có dạng nửa khối cầu. Biết hình nón có chiều cao \(h = 10\,cm\), còn bán kính khối cầu bằng bán kính đường tròn đáy r của hình nón, biết \(r = 3\,cm\). Tính gần đúng lượng kem cần để làm được \(100\) que kem ốc quế.

Cầu Tràng Tiền (thuộc thành phố Huế) là một công trình được xây vào thời Pháp thuộc. Tổng chiều dài của cây cầu là 402 mét và được chia làm 6 nhịp đều nhau. Vòng cung trên mỗi nhịp cầu là một phần đường tròn và có chiều dài bằng nhau. Chân mỗi nhịp cầu cao 1,85 mét và độ cao mỗi nhịp (tính từ điểm cao nhất của nhịp cầu đến mặt sàn cầu) là 5,45 mét. Tính tổng chiều dài của các nhịp cầu.

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

Câu hỏi: Cầu Tràng Tiền (thuộc thành phố Huế) là một công trình được xây vào thời Pháp thuộc. Tổng chiều dài của cây cầu là 402 mét và được chia làm 6 nhịp đều nhau. Vòng cung trên mỗi nhịp cầu là một phần đường tròn và có chiều dài bằng nhau. Chân mỗi nhịp cầu cao 1,85 mét và độ cao mỗi nhịp (tính từ điểm cao nhất của nhịp cầu đến mặt sàn cầu) là 5,45 mét. Tính tổng chiều … [Đọc thêm...] vềCầu Tràng Tiền (thuộc thành phố Huế) là một công trình được xây vào thời Pháp thuộc. Tổng chiều dài của cây cầu là 402 mét và được chia làm 6 nhịp đều nhau. Vòng cung trên mỗi nhịp cầu là một phần đường tròn và có chiều dài bằng nhau. Chân mỗi nhịp cầu cao 1,85 mét và độ cao mỗi nhịp (tính từ điểm cao nhất của nhịp cầu đến mặt sàn cầu) là 5,45 mét. Tính tổng chiều dài của các nhịp cầu.

Cho một cổ vật hình trụ có chiều cao đo được là \(81{\rm{cm}}\), do bị hư hại nên khi tiến hành đo đạc lại thu được \(AB = 50{\rm{cm}},BC = 70{\rm{cm}},CA = 80{\rm{cm}}\), với \(A,B,C\)thuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây?

Ngày Thuộc chủ đề:Trắc nghiệm Khối đa diện Tag với:,

Câu hỏi: Cho một cổ vật hình trụ có chiều cao đo được là \(81{\rm{cm}}\), do bị hư hại nên khi tiến hành đo đạc lại thu được \(AB = 50{\rm{cm}},BC = 70{\rm{cm}},CA = 80{\rm{cm}}\), với \(A,B,C\)thuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây? A. \(1,03{{\rm{m}}^{\rm{3}}}\). B. \(0,43{{\rm{m}}^{\rm{3}}}\). C. … [Đọc thêm...] vềCho một cổ vật hình trụ có chiều cao đo được là \(81{\rm{cm}}\), do bị hư hại nên khi tiến hành đo đạc lại thu được \(AB = 50{\rm{cm}},BC = 70{\rm{cm}},CA = 80{\rm{cm}}\), với \(A,B,C\)thuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây?

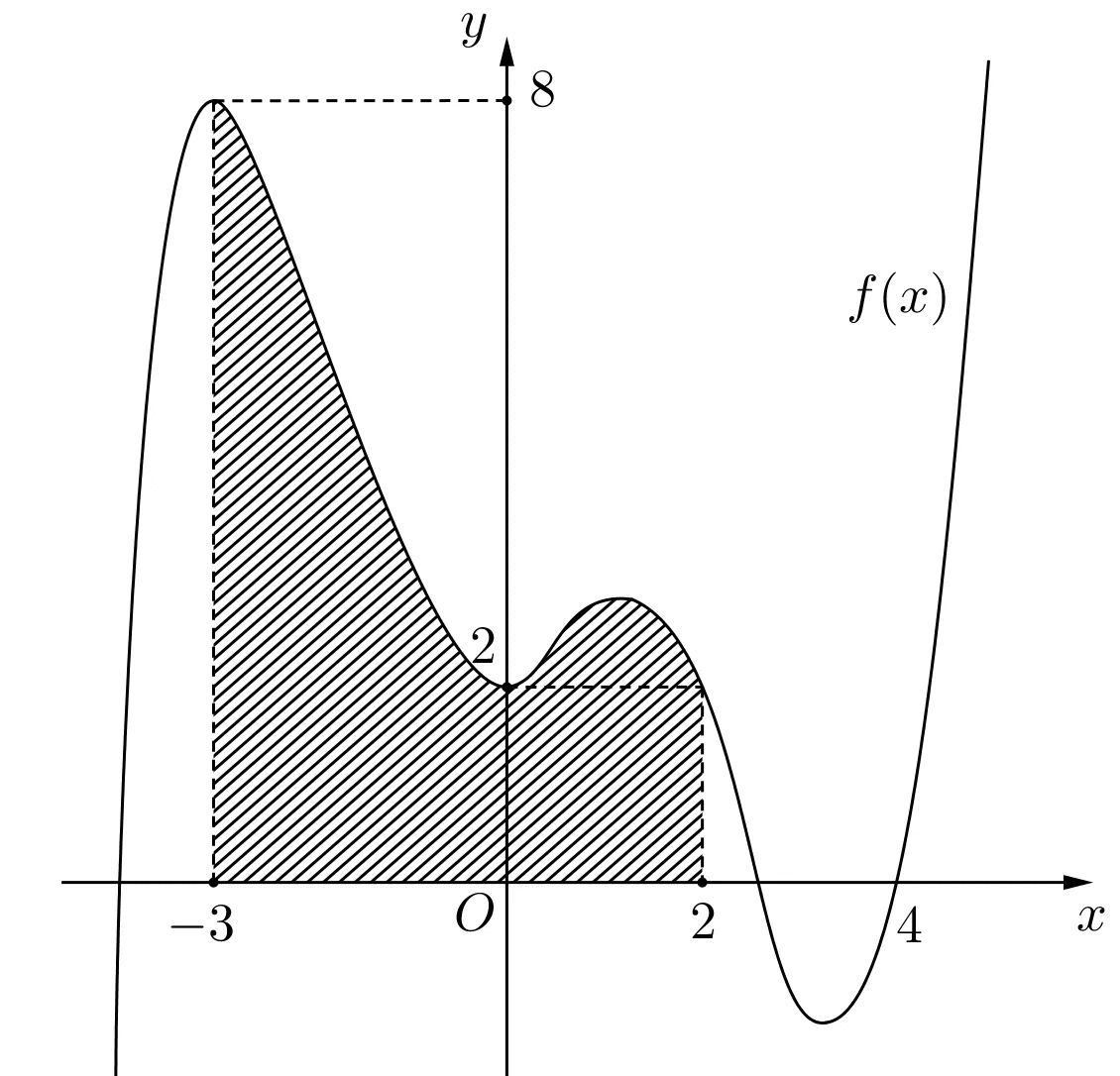
(THPT Lương Tài 2 – Bắc Ninh – 2022) Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ. Giả sử diện tích phần kẻ sọc trên hình vẽ có diện tích bằng \(a\). Tính theo \(a\) giá trị của tích phân \(I = \int\limits_{ – 3}^2 {\left( {2x + 1} \right)} f’\left( x \right)dx\)?

Diagram, histogram Description automatically generated

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:, ,

Câu hỏi: (THPT Lương Tài 2 - Bắc Ninh - 2022) Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ. Giả sử diện tích phần kẻ sọc trên hình vẽ có diện tích bằng \(a\). Tính theo \(a\) giá trị của tích phân \(I = \int\limits_{ - 3}^2 {\left( {2x + 1} \right)} f'\left( x \right)dx\)? A. \(I = 50 - 2a\). B. \(I = 50 - a\). C. … [Đọc thêm...] về

(THPT Lương Tài 2 – Bắc Ninh – 2022) Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ. Giả sử diện tích phần kẻ sọc trên hình vẽ có diện tích bằng \(a\). Tính theo \(a\) giá trị của tích phân \(I = \int\limits_{ – 3}^2 {\left( {2x + 1} \right)} f’\left( x \right)dx\)?

Diagram, histogram Description automatically generated

(THPT Phù Cừ – Hưng Yên – 2022) Cho hàm số \(y = f(x)\) có đồ thị hàm số \(y = f\prime (x)\) như hình vẽ.

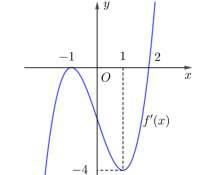
Số giá trị nguyên của tham số \(m\) để hàm số \(g(x) = f\left( {2{x^2} – 4|x| + m – 3} \right)\) có 7 điểm cực trị.

Ngày Thuộc chủ đề:Trắc nghiệm VDC Hàm số Tag với:,

Câu hỏi: (THPT Phù Cừ - Hưng Yên - 2022) Cho hàm số \(y = f(x)\) có đồ thị hàm số \(y = f\prime (x)\) như hình vẽ. Số giá trị nguyên của tham số \(m\) để hàm số \(g(x) = f\left( {2{x^2} - 4|x| + m - 3} \right)\) có 7 điểm cực trị. A. 1. B. 2. C. 4. D. 3. Lời giải: Ta có \(g\prime (x) = \left( {2{x^2} - 4|x| + m - 3} \right)\prime \cdot f\prime … [Đọc thêm...] về

(THPT Phù Cừ – Hưng Yên – 2022) Cho hàm số \(y = f(x)\) có đồ thị hàm số \(y = f\prime (x)\) như hình vẽ.

Số giá trị nguyên của tham số \(m\) để hàm số \(g(x) = f\left( {2{x^2} – 4|x| + m – 3} \right)\) có 7 điểm cực trị.

(Sở Phú Thọ 2022) Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ

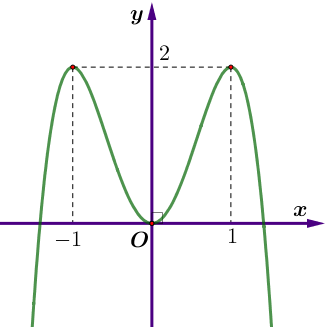
Số nghiệm thực phân biệt của phương trình \(2\left| {f\left( {x – 1 – 2\sqrt {x – 1} } \right)} \right| = 3\) là

Ngày Thuộc chủ đề:Trắc nghiệm VDC Hàm số Tag với:,

Câu hỏi: (Sở Phú Thọ 2022) Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ Số nghiệm thực phân biệt của phương trình \(2\left| {f\left( {x - 1 - 2\sqrt {x - 1} } \right)} \right| = 3\) là A. \(12\). B. \(5\). C. \(8\). D. \(4\). Lời giải: Chọn B Xét phương trình \(2\left| {f\left( {x - 1 - 2\sqrt {x - 1} } \right)} \right| = 3\) … [Đọc thêm...] về

(Sở Phú Thọ 2022) Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ

Số nghiệm thực phân biệt của phương trình \(2\left| {f\left( {x – 1 – 2\sqrt {x – 1} } \right)} \right| = 3\) là