Cho hình lăng trụ \(ABC.A’B’C’\) có đáy là tam giác đều. Hình chiếu vuông góc của \(A’\) trên mặt phẳng \((ABC)\) là trung điểm \(BC\). Mặt phẳng \((P)\) vuông góc với các cạnh bên và cắt các cạnh bên của hình lăng trụ lần lượt tại \(D,E,F\). Biết mặt phẳng \((ABB’A’)\) vuông góc với mặt phẳng \((ACC’A’)\) và chu vi tam giác \(DEF\) bằng 4, thể tích của khối lăng trụ \(ABC.A’B’C’\) bằng

Cho hình lăng trụ \(ABC.A’B’C’\) có đáy là tam giác đều. Hình chiếu vuông góc của \(A’\) trên mặt phẳng \((ABC)\) là trung điểm \(BC\). Mặt phẳng \((P)\) vuông góc với các cạnh bên và cắt các cạnh bên của hình lăng trụ lần lượt tại \(D,E,F\). Biết mặt phẳng \((ABB’A’)\) vuông góc với mặt phẳng \((ACC’A’)\) và chu vi tam giác \(DEF\) bằng 4, thể tích của khối lăng trụ \(ABC.A’B’C’\) bằng
A. \(12\left( {10 – 7\sqrt 2 } \right)\).

B. \(6\left( {10 – 7\sqrt 2 } \right)\).

C. \(12\left( {10 + 7\sqrt 2 } \right)\).

D. \(4\left( {10 + 7\sqrt 2 } \right)\).

Lời giải

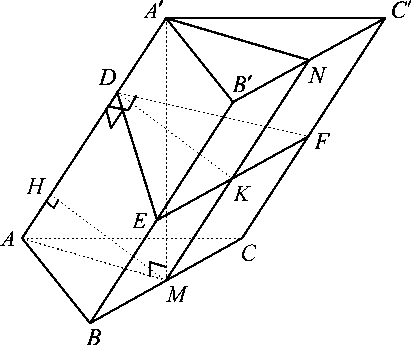
Gọi \(M,N\) lần lượt là trung điểm \(BC\)và \(B’C’\).
Gọi \(K\) là giao điểm \(MN\) và \(EF\).
Do \(\left\{ \begin{array}{l}BC \bot AM\\BC \bot A’M\end{array} \right. \Rightarrow BC \bot (AMNA’) \Rightarrow BC \bot AA’ \Rightarrow BC \bot BB’\)
Do \((DEF) \bot BB’ \Rightarrow EF \bot BB’\)
Trong mặt phẳng \((BCC’B’)\) có \(EF \bot BB’,BC \bot BB’ \Rightarrow BC{\rm{//}}EF\)
\( \Rightarrow K\) là trung điểm \(EF\).
Mặt khác \(BC \bot (AMNA’) \Rightarrow BC \bot DK \Rightarrow EF \bot DK\)
\( \Rightarrow \)Tam giác \(DEF\) là tam giác cân tại \(D\).
Do mặt phẳng \((ABB’A’)\) vuông góc với mặt phẳng \((ACC’A’)\) \( \Rightarrow \widehat {EDF} = 90^\circ \)
\( \Rightarrow \)Tam giác \(DEF\) là tam giác vuông cân tại \(D\).
Do chu vi tam giác \(DEF\) bằng 4 \( \Rightarrow DE + DF + EF = 4 \Leftrightarrow \frac{{EF}}{{\sqrt 2 }} + \frac{{EF}}{{\sqrt 2 }} + EF = 4 \Leftrightarrow EF = 4\left( {\sqrt 2 – 1} \right)\)
\( \Rightarrow BC = EF = 4\left( {\sqrt 2 – 1} \right)\).
Do tam giác \(ABC\) đều nên \(AM = BC.\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \left( {\sqrt 2 – 1} \right)\).
Kẻ \(MH \bot AA’ \Rightarrow MH = DK = \frac{1}{2}EF = 2\left( {\sqrt 2 – 1} \right)\)
Xét tam giác vuông \(A’MA\) ta có:
\(\frac{1}{{M{H^2}}} = \frac{1}{{M{A^2}}} + \frac{1}{{A'{M^2}}} \Leftrightarrow \frac{1}{{4{{\left( {\sqrt 2 – 1} \right)}^2}}} = \frac{1}{{12\left( {\sqrt 2 – {1^2}} \right)}} + \frac{1}{{A'{M^2}}} \Leftrightarrow \frac{1}{{A'{M^2}}} = \frac{1}{{6{{\left( {\sqrt 2 – 1} \right)}^2}}}\)
\( \Rightarrow A’M = \sqrt 6 .\left( {\sqrt 2 – 1} \right)\).
Vậy \({V_{ABC.A’B’C’}} = {S_{ABC}}.A’M = \frac{1}{2}AM.BC.A’M = 12.\left( {10 – 7\sqrt 2 } \right)\).