Hằng ngày mực nước của một con kênh lên xuống theo thủy triều. Độ sâu $h\left( \text{m} \right)$ của mực nước trong kênh tại thời điểm $t\left( \text{h} \right)\left( 0\le t\le 24 \right)$ trong ngày được xác định bởi công thức $h=2\cos \left( \dfrac{\pi t}{12}+\dfrac{\pi }{3} \right)+5$

Đáp án: 28

Lời giải:
Ta có $h\left( t \right)=2\cos \left( \dfrac{\pi t}{12}+\dfrac{\pi }{3} \right)+5$ $\Rightarrow {h}’\left( t \right)=-\dfrac{\pi }{6}\sin \left( \dfrac{\pi t}{12}+\dfrac{\pi }{3} \right)$. ${h}’\left( t \right)=0\Leftrightarrow \sin \left( \dfrac{\pi t}{12}+\dfrac{\pi }{3} \right)=0\Leftrightarrow \dfrac{\pi t}{12}+\dfrac{\pi }{3}=k\pi$ $\Leftrightarrow t=-4+12k\left( k\in \mathbb{Z} \right)$. Mà $0\le t\le 24$ nên $0\le -4+12k\le 24\Leftrightarrow \dfrac{1}{3}\le k\le \dfrac{7}{3}$ $\Rightarrow k\in \left\{ 1;2 \right\}$. Do đó ${h}’\left( t \right)=0\Rightarrow \left[ \begin{array}{l} t=8 \\ t=20 \end{array} \right.$

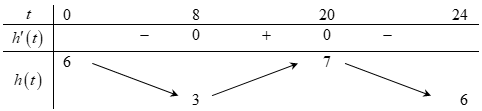
$\Rightarrow h\left( t \right)$ đồng biến trên khoảng $\left( 8;20 \right)$ hay trong khoảng từ $8\text{h}$ đến $20\text{h}$ độ sâu của mực nước trong kênh tăng dần. Vậy $a=8;b=20$ và $a+b=28$.