Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ $t$ là ${f(t)=180 t+42 t^2-t^3, t=0,1, \ldots, 30}$

Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ $t$ là ${f(t)=180 t+42 t^2-t^3, t=0,1, \ldots, 30}$. Nếu coi ${f(t)}$ là hàm số xác định trên đoạn ${[0 ; 30]}$ thì đạo hàm ${f^{\prime}(t)}$ được xem là tốc độ truyền bệnh (đơn vị: người/ngày) tại thời điểm ${t}$. Hỏi trong 30 ngày đó, có bao nhiêu ngày mà tốc độ truyền bệnh giảm?

Lời giải

Trả lời: 16.

Ta có:

${{f}^{\prime }}(t)=180+84t-3{{t}^{2}};{{f}^{\prime \prime }}(t)=84-6t;{{f}^{\prime \prime }}(t)=0\Leftrightarrow t=14.$

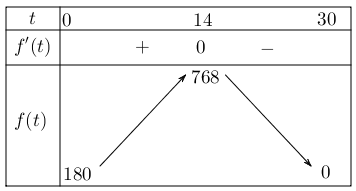
Do đó trong khoảng ${(14 ; 30)}$ tức là từ ngày thứ 15 đến ngày thứ 30, thì tốc độ truyền bệnh giảm.

Do đó có ${30-15+1=16}$ ngày mà tốc độ truyền bệnh giảm.