Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery

Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm ${t=0({~s})}$ cho đến khi tên lửa đẩy được phóng đi tại thời điểm ${t=26}$ (s) được cho bởi hàm số sau: $v$ được tính bằng $ft/s,1\text{ feet }=0,3048~m.$

Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi? Kết quả thời gian được tính bằng giây và làm tròn đến hàng phần mười

Lời giải:

Trả lời: 23,1

Gia tốc tàu con thoi là ${a(t)=3,906 \cdot 10^{-3} t^2-0,18058 t}$; ${{a}^{\prime }}(t)=7,812\cdot {{10}^{-3}}t-0,18058;{{a}^{\prime }}(t)=0\Rightarrow t=\frac{0,18058}{7,812\cdot {{10}^{-3}}}\approx 23,116$

Bảng biến thiên hàm gia tốc:

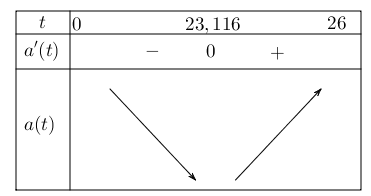
Vậy kể từ thời điểm ${t}$ xấp xỉ với 23,116 (s) thì gia tốc của tàu con thoi sẽ tăng.