Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hoá bằng hàm số $N\left( t \right)=-{{t}^{3}}+12{{t}^{2}}$, $0\le t\le 12$, trong đó $N$ là số người bị nhiễm bệnh (đơn vị là trăm người) và $t$ là thời gian (tuần)

Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hoá bằng hàm số $N\left( t \right)=-{{t}^{3}}+12{{t}^{2}}$, $0\le t\le 12$, trong đó $N$ là số người bị nhiễm bệnh (đơn vị là trăm người) và $t$ là thời gian (tuần). Gọi $\left( a\,;b \right)$ là khoảng thời gian lâu nhất mà số người bị nhiễm bệnh tăng lên. Tính giá trị $P=2{{a}^{2}}-{{b}^{2}}$.

Lời giải

Đáp án: $-64$.

Ta có $N'(t)=-3{{t}^{2}}+24t=0\Rightarrow t=0\,;t=8$. Bảng biến thiên như sau:

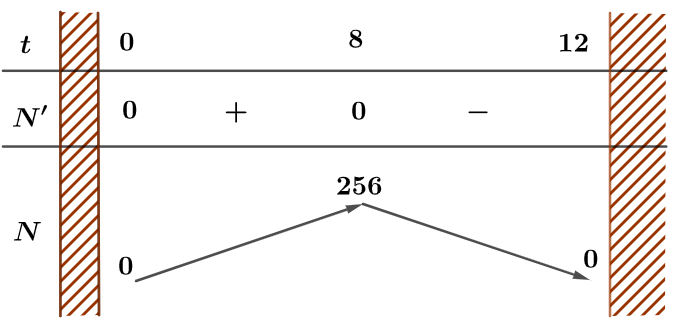
Số người bị nhiễm bệnh tăng trên khoảng thời gian $(0\,;8)$.

Vậy $P=2\cdot {{0}^{2}}-{{8}^{2}}=-64$.