Một khách sạn có 50 phòng cho thuê

Một khách sạn có 50 phòng cho thuê. Giả sử doanh thu (tức là tổng số tiền thu được) là ${T(x)=-\frac{1}{38} x^2+2 x}$ (triệu đồng) với ${x}$ là số phòng cho thuê được. Hỏi có bao nhiêu giá trị nguyên dương của ${x}$ nằm trong miền doanh thu ${T(x)}$ tăng?

Lời giải

Trả lời: 38.

Ta có: ${T^{\prime}(x)=-\frac{1}{19} x+2 ; T^{\prime}(x)=0 \Leftrightarrow x=38}$.

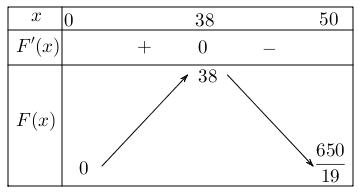
Khi đó, với ${x \in(0 ; 38]}$ thì ${T(x)}$ tăng.

Vậy có 38 giá trị nguyên dương ${x}$ thoả mãn.