Một con cá bơi ngược dòng để vượt khoảng cách $250km$. Vận tốc dòng nước là ${5 {~km} / {h}}$. Nếu vận tốc boi của cá khi nước đứng yên là ${v({~km} / {h})}$ thì năng lượng tiêu hao của cá trong ${t}$ giờ được cho bởi công thức ${E(v)=c v^3 t}$, trong đó ${c}$ là một hằng số và năng lượng ${E}$ tính bằng Jun. Khi vận tốc bơi của cá nằm trong khoảng (${m ; n}$) lớn nhất ( ${m, n}$ là số nguyên hoặc là phân số tối giản) thì năng lượng tiêu hao của cá giảm. Tính ${m+2 n}$.

Lời giải
Trả lời: 20
Vận tốc của cá khi bơi ngược dòng nước là ${v-5}$ ${(k m / h)}$. Điều kiện: ${v>5}$.
Thời gian để cá vượt qua quãng đường 250 km là $t=\frac{250}{v-5}$ (giờ).
Năng lượng tiêu hao của cá để vượt qua quãng đường đó là ${E(v)=c v^3 \cdot \frac{250}{v-5}}$ (Jun).
Ta có: ${E^{\prime}(v)=250 c \cdot \frac{2 v^3-15 v^2}{(v-5)^2}}$; ${E^{\prime}(v)=0 \Leftrightarrow v=0}$ (loại) hoặc ${v=\frac{15}{2}}$.
Bảng biến thiên:
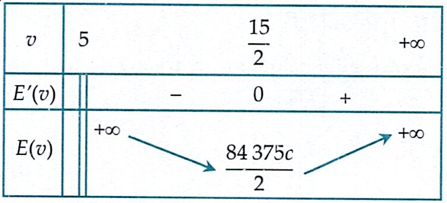
Khi đó vận tốc bơi của cá nằm trong khoảng ${\left(5 ; \frac{15}{2}\right)}$ thì năng lượng tiêu hao của cá giảm.
Vậy ${m=5 ; n=\frac{15}{2} \Rightarrow m+2 n=20}$.
