Giả sử lợi nhuận của một cửa hàng tạp hoá nhỏ trong ngày thứ ${x}$ của một tháng nào đó được cho bơi công thức ${h(x)=-2 x^2+40 x+700}$ (đơn vị: nghìn đồng)

Giả sử lợi nhuận của một cửa hàng tạp hoá nhỏ trong ngày thứ ${x}$ của một tháng nào đó được cho bơi công thức ${h(x)=-2 x^2+40 x+700}$ (đơn vị: nghìn đồng). Giả sử tháng đó có 30 ngày, hỏi có bao nhiêu ngày trong tháng đó cửa hàng có lợi nhuận tăng so với lợi nhuận ngày liền trước đó?

Lời giải

Trả lời: 9

Ta có: ${h^{\prime}(x)=-4 x+40 ; h^{\prime}(x)=0 \Leftrightarrow x=10}$.

Bảng biến thiên của ${h(x)}$ trên đoạn ${[1 ; 30]}$:

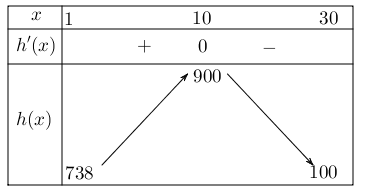
Dựa vào bảng biến thiên, ta thấy hàm lợi nhuận ${h(x)}$ có giá trị tăng trên đoạn ${[1 ; 10]}$. Do đó các ngày có lợi nhuận tăng so với ngày liền trước đó là từ ngày 2 đến ngày 10.

Vậy có ${10-2+1=9}$ ngày.