Một cửa hàng quần áo đã thống kê số lượng quần áo bán ra trong ngày thứ ${x(1 \leq x \leq 30)}$ của một tháng xác định tuân theo quy luật được mô hình hoá bởi hàm số ${f(x)=3 x^2-54 x+256}$. Hỏi trong tháng đó, có bao nhiêu ngày có số lượng quần áo bán ra nhiều hơn ngày hôm trước?
Lời giải
Trả lời: 21
Ta có: ${f^{\prime}(x)=6 x-54 ; f^{\prime}(x)=0 \Leftrightarrow x=9}$
Ta có bảng biến thiên:
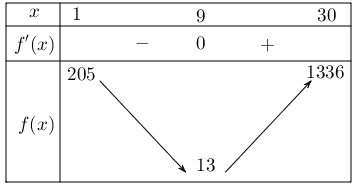
Vậy, các ngày trong tháng có số lượng quần áo bán ra nhiều hơn ngày hôm trước là từ ngày 10 đến ngày 30.
Khi đó có ${30-10+1=21}$ ngày thoả mãn yêu cầu bài toán.
