Trên một trục số thẳng đứng có chiều dương hướng lên trên, một chất điểm bắt đầu chuyển động dọc theo trục số.
Giả sử, tại thời điểm $t$ giây $(t \ge 0))$ tính từ lúc bắt đầu chuyển động thì vị trí $s(t)$ của chất điểm trên trục số thẳng đứng được xác định bởi công thức $s(t)=\frac{t^{3}}{3} – 12 t^{2} + 135 t$ mét.
Trong $24$ giây chuyển động đầu tiên chất điểm di chuyển được tổng quãng đường bằng bao nhiêu mét?
Giả sử, tại thời điểm $t$ giây $(t \ge 0))$ tính từ lúc bắt đầu chuyển động thì vị trí $s(t)$ của chất điểm trên trục số thẳng đứng được xác định bởi công thức $s(t)=\frac{t^{3}}{3} – 12 t^{2} + 135 t$ mét.
Trong $24$ giây chuyển động đầu tiên chất điểm di chuyển được tổng quãng đường bằng bao nhiêu mét?
Đáp án: 1008
Lời giải:
Ta có $s'(t)=t^{2} – 24 t + 135$. $s'(t)=0 \Leftrightarrow t^{2} – 24 t + 135=0 \Leftrightarrow \left[\begin{array}{l} t=9 \\ t=15.\end{array}\right.$ Bảng biến thiên
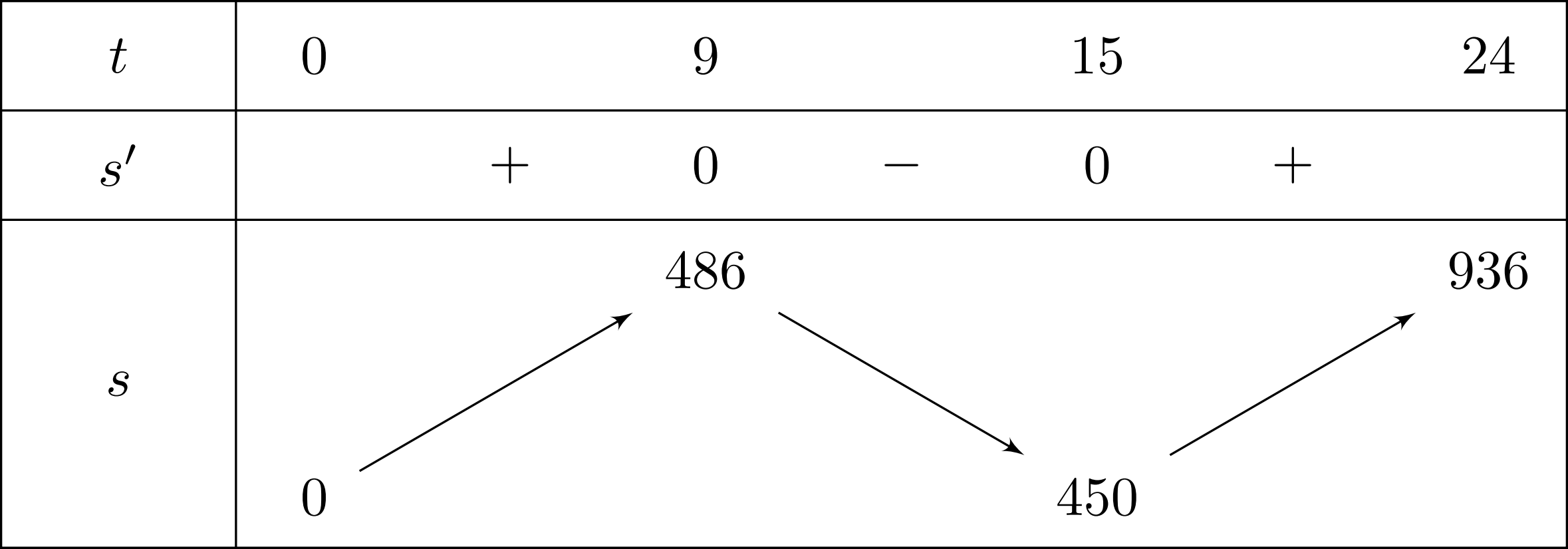
Trong $9$ giây đầu tiên, chất điểm di chuyển hướng lên $486$ mét. Trong khoảng (9;15) giây tiếp theo, chất điểm di chuyển hướng xuống $36$ mét. Trong khoảng (15;24) giây cuối, chất điểm di chuyển hướng lên $486$ mét. Vậy trong $24$ giây đầu tiên chất điểm chuyển động được quãng đường là $486+36+486=1008$ mét.
