Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Trắc nghiệm Tính đơn điệu của hàm số

Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = x{\left( {x – 1} \right)^2}{\left( {x + 1} \right)^3}\left( {x – 2} \right)\). Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:

Câu hỏi: Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x - 1} \right)^2}{\left( {x + 1} \right)^3}\left( {x - 2} \right)\). Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây? A. \(\left( {1; + \infty } \right)\). B. \(\left( { - 1;0} \right)\). C. \(\left( { - \infty ; - 1} \right)\). D. \(\left( {0;1} … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = x{\left( {x – 1} \right)^2}{\left( {x + 1} \right)^3}\left( {x – 2} \right)\). Hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?

Cho hàm số\(y = f\left( x \right)\) có bảng xét dấu của đạo hàm \(y = f’\left( x \right)\)như sau
Hàm số \(y = 3f\left( { – x + 2} \right) + {x^3} + 3{x^2} – 9x + 1\) nghịch biến trên khoảng nào sau đây?

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:

Câu hỏi: Cho hàm số\(y = f\left( x \right)\) có bảng xét dấu của đạo hàm \(y = f'\left( x \right)\)như sau Hàm số \(y = 3f\left( { - x + 2} \right) + {x^3} + 3{x^2} - 9x + 1\) nghịch biến trên khoảng nào sau đây? A. \(\left( { - 2;1} \right)\). B. \(\left( {2; + \infty } \right)\). C. \(\left( {0;2} \right)\). D. \(\left( { - \infty ; - 2} \right)\). LỜI … [Đọc thêm...] vềCho hàm số\(y = f\left( x \right)\) có bảng xét dấu của đạo hàm \(y = f’\left( x \right)\)như sau

Hàm số \(y = 3f\left( { – x + 2} \right) + {x^3} + 3{x^2} – 9x + 1\) nghịch biến trên khoảng nào sau đây?

Tìm tất cả các khoảng nghịch biến của hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:

Câu hỏi: Tìm tất cả các khoảng nghịch biến của hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\). A. \(\left( { - \infty ; - 1} \right)\) và \(\left( { - 1; + \infty } \right)\). B. \(\left( { - 2; - 1} \right)\) và \(\left( { - 1;0} \right)\). C. \(\left( { - \infty ; - 2} \right)\) và \(\left( {0; + \infty } \right)\). D. \(\left( { - 2;0} \right)\). LỜI GIẢI … [Đọc thêm...] vềTìm tất cả các khoảng nghịch biến của hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\).

Cho hàm số \(f\left( x \right)\) có bảng xét dấu đạo hàm như sau:
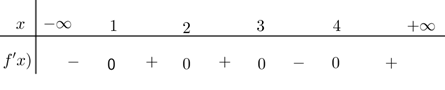
Hàm số \(y = f\left( {3x + 1} \right) – {x^3} + 3x\) đồng biến trên khoảng nào dưới đây?

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:

Câu hỏi: Cho hàm số \(f\left( x \right)\) có bảng xét dấu đạo hàm như sau: Hàm số \(y = f\left( {3x + 1} \right) - {x^3} + 3x\) đồng biến trên khoảng nào dưới đây? A. \(\left( { - 1\,;\, - \frac{1}{3}} \right)\). B. \(\left( {\frac{1}{4}\,;\,\frac{1}{3}} \right)\). C. \(\left( {\frac{2}{3}\,;\,1} \right)\). D. \(\left( {\frac{3}{4}\,;1} \right)\) LỜI GIẢI … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) có bảng xét dấu đạo hàm như sau:

Hàm số \(y = f\left( {3x + 1} \right) – {x^3} + 3x\) đồng biến trên khoảng nào dưới đây?

Hàm số nào dưới đây đồng biến trên \(\mathbb{R}\)?

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:

Câu hỏi: Hàm số nào dưới đây đồng biến trên \(\mathbb{R}\)? A. \(y = {x^4} + {x^2}\) B. \(y = {x^4} - x\) C. \(y = {x^3} + x\) D. \(y = {x^3} - {x^2}\) LỜI GIẢI CHI TIẾT Ta có: \(y = {x^3} + x\); \(y' = 3{x^2} + 1\)\( > 0\)với \(\forall x \in \mathbb{R}\). Do đó hàm số \(y = {x^3} + x\) đồng biến trên \(\mathbb{R}\). ======= Thuộc mục: Trắc … [Đọc thêm...] vềHàm số nào dưới đây đồng biến trên \(\mathbb{R}\)?

Hàm số \(y = {x^3} – 3{x^2} + 1 \) nghịch biến trên khoảng nào?

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:

Câu hỏi: Hàm số \(y = {x^3} - 3{x^2} + 1 \) nghịch biến trên khoảng nào? A. \(\left( {2: + \infty } \right)\). B. \(\left( { - \infty ;0} \right)\) và \(\left( {2: + \infty } \right)\). C. \(\left( {0;{\mkern 1mu} 2} \right)\). D. \(\left( { - \infty ;0} \right)\). LỜI GIẢI CHI TIẾT Ta có \(y' = 3{x^2} - 6x = 0 \Leftrightarrow x = 0;x = … [Đọc thêm...] vềHàm số \(y = {x^3} – 3{x^2} + 1 \) nghịch biến trên khoảng nào?

Hàm số \(y = {\left( {{x^2} – x} \right)^2}\) nghịch biến trên khoảng nào dưới đây?

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:

Câu hỏi: Hàm số \(y = {\left( {{x^2} - x} \right)^2}\) nghịch biến trên khoảng nào dưới đây? A. \(\left( {1;2} \right)\). B. \(\left( { - 2;0} \right)\). C. \(\left( {0;1} \right)\). D. \(\left( {0;\frac{1}{2}} \right)\). LỜI GIẢI CHI TIẾT Ta có \(y' = 2\left( {{x^2} - x} \right)\left( {2x - 1} \right)\). Giải phương trình \(y' = 0\)\( \Leftrightarrow … [Đọc thêm...] vềHàm số \(y = {\left( {{x^2} – x} \right)^2}\) nghịch biến trên khoảng nào dưới đây?

Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f’\left( x \right) = \left( {x – 1} \right){\left( {x – 2} \right)^2}{\left( {x – 3} \right)^{2017}}\).Khẳng định nào dưới đây đúng?

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:

Câu hỏi: Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = \left( {x - 1} \right){\left( {x - 2} \right)^2}{\left( {x - 3} \right)^{2017}}\).Khẳng định nào dưới đây đúng? A. Hàm số nghịch biến trên khoảng \(\left( {1;3} \right)\). B. Hàm số đạt cực đại tại \(x = 2\) và đạt cực tiểu tại \(x = 1\) và \(x = 3\). C. … [Đọc thêm...] vềCho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f’\left( x \right) = \left( {x – 1} \right){\left( {x – 2} \right)^2}{\left( {x – 3} \right)^{2017}}\).Khẳng định nào dưới đây đúng?

Cho hàm số \(y = \frac{{{x^2} – 1}}{x}\). Khẳng định nào sau đây là khẳng định đúng.

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:

Câu hỏi: Cho hàm số \(y = \frac{{{x^2} - 1}}{x}\). Khẳng định nào sau đây là khẳng định đúng. A. Hàm số đã cho chỉ đồng biến trên \(\left( { - \infty ;0} \right)\). B. Hàm số đã cho đồng biến trên \(\mathbb{R}\backslash \left\{ 0 \right\}\). C. Hàm số đã cho chỉ đồng biến trên \(\left( {0; + \infty } \right)\). D. Hàm số đã cho đồng biến trên mỗi khoảng xác … [Đọc thêm...] vềCho hàm số \(y = \frac{{{x^2} – 1}}{x}\). Khẳng định nào sau đây là khẳng định đúng.

Cho hàm số \(y = – \frac{1}{3}{x^3} – m{x^2} + \left( {3m + 2} \right)x – 2020\). Tìm tất cả các giá trị của tham số \(m\) để hàm số nghịch biến trên khoảng \(\left( { – \infty ; + \infty } \right)\).

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:

Câu hỏi: Cho hàm số \(y = - \frac{1}{3}{x^3} - m{x^2} + \left( {3m + 2} \right)x - 2020\). Tìm tất cả các giá trị của tham số \(m\) để hàm số nghịch biến trên khoảng \(\left( { - \infty ; + \infty } \right)\). A. \(\left[ \begin{array}{l}m \ge 2\\m \le - 1\end{array} \right.\). B. \(m \le 2\). C. \( - 2 \le m \le - 1\). D. \( - 1 \le m \le 0\). LỜI GIẢI CHI … [Đọc thêm...] vềCho hàm số \(y = – \frac{1}{3}{x^3} – m{x^2} + \left( {3m + 2} \right)x – 2020\). Tìm tất cả các giá trị của tham số \(m\) để hàm số nghịch biến trên khoảng \(\left( { – \infty ; + \infty } \right)\).