Tìm tâm, bán kính phương trình mặt cầu ========== Câu 13: Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):\,{\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 3} \right)^2} = 16\). Tâm của \(\left( S \right)\) có tọa độ là A. \(\left( { - 1\,;\, - 2\,;\, - 3} \right)\). B. \(\left( {1\,;\,2\,;\,3} \right)\). C. \(\left( { - 1\,;\,2\,;\, … [Đọc thêm...] vềTìm tâm, bán kính phương trình mặt cầu
Trắc nghiệm Phương trình mặt cầu và các dạng toán liên quan
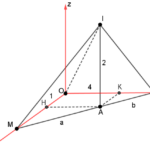
Đề toán 2022 Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) tâm \(I\left( {1;4;2} \right)\), bán kính bằng 2. Gọi \(M,N\) là hai điểm lần lượt thuộc hai trục \(Ox,Oy\) sao cho đường thẳng \(MN\) tiếp xúc với \(\left( S \right)\), đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{7}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và \(\left( S \right)\), giá trị \(AM.AN\) bằng
Đề toán 2022 Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) tâm \(I\left( {1;4;2} \right)\), bán kính bằng 2. Gọi \(M,N\) là hai điểm lần lượt thuộc hai trục \(Ox,Oy\) sao cho đường thẳng \(MN\) tiếp xúc với \(\left( S \right)\), đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{7}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và \(\left( S … [Đọc thêm...] về Đề toán 2022 Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) tâm \(I\left( {1;4;2} \right)\), bán kính bằng 2. Gọi \(M,N\) là hai điểm lần lượt thuộc hai trục \(Ox,Oy\) sao cho đường thẳng \(MN\) tiếp xúc với \(\left( S \right)\), đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{7}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và \(\left( S \right)\), giá trị \(AM.AN\) bằng
Đề toán 2022 [2H3-3.3-4] Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) tâm \(I\left( {4\,;\,1\,;\,2} \right)\) bán kính bằng 2. Gọi \(M,N\) là hai điểm lần lượt thuộc hai trục \(Ox,Oy\) sao cho đường thẳng \(MN\) tiếp xúc với \(\left( S \right)\), đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{7}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và \(\left( S \right)\), giá trị của \(AM.AN\) bằng.
Đề toán 2022 [2H3-3.3-4] Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) tâm \(I\left( {4\,;\,1\,;\,2} \right)\) bán kính bằng 2. Gọi \(M,N\) là hai điểm lần lượt thuộc hai trục \(Ox,Oy\) sao cho đường thẳng \(MN\) tiếp xúc với \(\left( S \right)\), đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{7}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và … [Đọc thêm...] về Đề toán 2022 [2H3-3.3-4] Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) tâm \(I\left( {4\,;\,1\,;\,2} \right)\) bán kính bằng 2. Gọi \(M,N\) là hai điểm lần lượt thuộc hai trục \(Ox,Oy\) sao cho đường thẳng \(MN\) tiếp xúc với \(\left( S \right)\), đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{7}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và \(\left( S \right)\), giá trị của \(AM.AN\) bằng.
Đề toán 2022 [ Mức độ 4] Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) tâm \(I\left( {1;\,3;\,9} \right)\) bán kính bằng \(3\). Gọi \(M\), \(N\) là hai điểm lần lượt thuộc hai trục \(Ox\), \(Oz\) sao cho đường thẳng \(MN\) tiếp xúc với \(\left( S \right)\), đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{{13}}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và \(\left( S \right)\), giá trị \(AM.AN\) bằng
Đề toán 2022 [ Mức độ 4] Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) tâm \(I\left( {1;\,3;\,9} \right)\) bán kính bằng \(3\). Gọi \(M\), \(N\) là hai điểm lần lượt thuộc hai trục \(Ox\), \(Oz\) sao cho đường thẳng \(MN\) tiếp xúc với \(\left( S \right)\), đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{{13}}{2}\). Gọi \(A\) là tiếp điểm … [Đọc thêm...] về Đề toán 2022 [ Mức độ 4] Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right)\) tâm \(I\left( {1;\,3;\,9} \right)\) bán kính bằng \(3\). Gọi \(M\), \(N\) là hai điểm lần lượt thuộc hai trục \(Ox\), \(Oz\) sao cho đường thẳng \(MN\) tiếp xúc với \(\left( S \right)\), đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{{13}}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và \(\left( S \right)\), giá trị \(AM.AN\) bằng
Đề toán 2022 Trong không gian \(Oxyz\), cho mặt cầu \((S)\) tâm \(I(9;3;1)\) bán kính bằng 3. Gọi \(M\), \(N\) là hai điểm lần lượt thuộc hai trục \(Ox\), \(Oz\) sao cho đường thẳng \(MN\) tiếp xúc với \((S)\),đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{{13}}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và \((S)\), giá trị \(AM.AN\) bằng
Đề toán 2022 Trong không gian \(Oxyz\), cho mặt cầu \((S)\) tâm \(I(9;3;1)\) bán kính bằng 3. Gọi \(M\), \(N\) là hai điểm lần lượt thuộc hai trục \(Ox\), \(Oz\) sao cho đường thẳng \(MN\) tiếp xúc với \((S)\),đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{{13}}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và \((S)\), giá trị \(AM.AN\) bằng
A. \(12\sqrt 3 … [Đọc thêm...] về Đề toán 2022 Trong không gian \(Oxyz\), cho mặt cầu \((S)\) tâm \(I(9;3;1)\) bán kính bằng 3. Gọi \(M\), \(N\) là hai điểm lần lượt thuộc hai trục \(Ox\), \(Oz\) sao cho đường thẳng \(MN\) tiếp xúc với \((S)\),đồng thời mặt cầu ngoại tiếp tứ diện \(OIMN\) có bán kính bằng \(\frac{{13}}{2}\). Gọi \(A\) là tiếp điểm của \(MN\) và \((S)\), giá trị \(AM.AN\) bằng
Điều kiện để \(\left( S \right):{x^2} + {y^2} + {z^2} + Ax + By + Cz + D = 0\) là một mặt cầu là:
Câu hỏi: Điều kiện để \(\left( S \right):{x^2} + {y^2} + {z^2} + Ax + By + Cz + D = 0\) là một mặt cầu là: A. \({A^2} + {B^2} + {C^2} - D > 0\) B. \({A^2} + {B^2} + {C^2} - 2D = 0\) C. \({A^2} + {B^2} + {C^2} - 4D > 0\) D. \({A^2} + {B^2} + {C^2} + D = 0\) Lời Giải: Đây là các bài toán toạ độ Mặt cầu trong phần Hình học OXYZ. \(\left( S \right):{x^2} … [Đọc thêm...] vềĐiều kiện để \(\left( S \right):{x^2} + {y^2} + {z^2} + Ax + By + Cz + D = 0\) là một mặt cầu là:
Với điều kiện nào của m thì mặt phẳng cong sau là mặt cầu? \(\left( S \right):{x^2} + {y^2} + {z^2} + 2\left( {3 – m} \right)x – 3\left( {m + 1} \right)y – 2mz + 2{m^2} + 7 = 0\)
Câu hỏi: Với điều kiện nào của m thì mặt phẳng cong sau là mặt cầu? \(\left( S \right):{x^2} + {y^2} + {z^2} + 2\left( {3 - m} \right)x - 3\left( {m + 1} \right)y - 2mz + 2{m^2} + 7 = 0\) A. \(m < 2 \vee \,\,m > 3\) B. \(1 \le m \le 3\) C. \(m < 1\, \vee \,m < 3\) D. \(m = 1\, \vee \,\,m = 3\) Lời Giải: Đây là các bài toán toạ độ Mặt cầu trong … [Đọc thêm...] vềVới điều kiện nào của m thì mặt phẳng cong sau là mặt cầu? \(\left( S \right):{x^2} + {y^2} + {z^2} + 2\left( {3 – m} \right)x – 3\left( {m + 1} \right)y – 2mz + 2{m^2} + 7 = 0\)
Giá trị \(\alpha\) phải thỏa mãn điều kiện nào để mặt cong là mặt cầu: \(\left( S \right):{x^2} + {y^2} + {z^2} + 2\left( {3 – {{\cos }^2}\alpha } \right)x + 4\left( {{{\sin }^2}\alpha – 1} \right) + 2z + \cos 4\alpha + 8 = 0\)? \((k\in Z)\)
Câu hỏi: Giá trị \(\alpha\) phải thỏa mãn điều kiện nào để mặt cong là mặt cầu: \(\left( S \right):{x^2} + {y^2} + {z^2} + 2\left( {3 - {{\cos }^2}\alpha } \right)x + 4\left( {{{\sin }^2}\alpha - 1} \right) + 2z + \cos 4\alpha + 8 = 0\)? \((k\in Z)\) A. \(\frac{{2\pi }}{3} + k2\pi < \alpha < \frac{{4\pi }}{3} + k2\pi \) B. \(\frac{\pi }{3} + k2\pi < \alpha … [Đọc thêm...] vềGiá trị \(\alpha\) phải thỏa mãn điều kiện nào để mặt cong là mặt cầu: \(\left( S \right):{x^2} + {y^2} + {z^2} + 2\left( {3 – {{\cos }^2}\alpha } \right)x + 4\left( {{{\sin }^2}\alpha – 1} \right) + 2z + \cos 4\alpha + 8 = 0\)? \((k\in Z)\)
Giá trị t phải thỏa mãn điều kiện nào để mặt cong sau là mặt cầu: \(\left( S \right):{x^2} + {y^2} + {z^2} + 2\left( {2 – \ln t} \right)x + 4\ln t.y + 2\left( {\ln t + 1} \right)z + 5{\ln ^2}t + 8 = 0\)
Câu hỏi: Giá trị t phải thỏa mãn điều kiện nào để mặt cong sau là mặt cầu: \(\left( S \right):{x^2} + {y^2} + {z^2} + 2\left( {2 - \ln t} \right)x + 4\ln t.y + 2\left( {\ln t + 1} \right)z + 5{\ln ^2}t + 8 = 0\) A. \(t < \frac{1}{e} \vee t > 3e\) B. \(\frac{1}{e} < t < 3e\) C. \(e < t < {e^3}\) D. \(0 < t < \frac{1}{e} \vee t > … [Đọc thêm...] vềGiá trị t phải thỏa mãn điều kiện nào để mặt cong sau là mặt cầu: \(\left( S \right):{x^2} + {y^2} + {z^2} + 2\left( {2 – \ln t} \right)x + 4\ln t.y + 2\left( {\ln t + 1} \right)z + 5{\ln ^2}t + 8 = 0\)
Cho hai điểm \(A\left( {2, – 3, – 1} \right);\,\,\,B\left( { – 4,5, – 3} \right)\). Định k để tập hợp các điểm M(x;y;z) sao cho \(A{M^2} + B{M^2} = 2\left( {{k^2} + 1} \right),\,\,k \in {R^ + }\) là một mặt cầu
Câu hỏi: Cho hai điểm \(A\left( {2, - 3, - 1} \right);\,\,\,B\left( { - 4,5, - 3} \right)\). Định k để tập hợp các điểm M(x;y;z) sao cho \(A{M^2} + B{M^2} = 2\left( {{k^2} + 1} \right),\,\,k \in {R^ + }\) là một mặt cầu A. 0 < k < 5 B. k = 5 C. k > 5 D. \(5 < k < \sqrt {21} \) Lời Giải: Đây là các bài toán toạ độ Mặt cầu trong phần Hình học … [Đọc thêm...] vềCho hai điểm \(A\left( {2, – 3, – 1} \right);\,\,\,B\left( { – 4,5, – 3} \right)\). Định k để tập hợp các điểm M(x;y;z) sao cho \(A{M^2} + B{M^2} = 2\left( {{k^2} + 1} \right),\,\,k \in {R^ + }\) là một mặt cầu