Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Trắc nghiệm Hình học OXYZ

Từ \(A\) kẻ các tiếp tuyến đến mặt cầu \(\left( S \right)\), gọi \(\left( P \right)\) là mặt phẳng chứa các tiếp điểm, biết \(\left( P \right)\) luôn đi qua một đường thẳng \(d\) cố định. Phương trình đường thẳng \(d\) là:

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:,

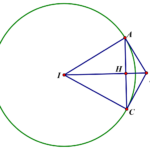
Trong không gian \(Oxyz\), cho mặt cầu \(\left( S \right):{x^2} + {\left( {y + 3} \right)^2} + {z^2} = 36\) và điểm \(A\) nằm trên đường thẳng \(\Delta \) có phương trình \(\left\{ \begin{array}{l}x = 1 - t\\y = 3\\z = 1 - t\end{array} \right.\) và nằm ngoài mặt cầu \(\left( S \right)\). Từ \(A\) kẻ các tiếp tuyến đến mặt cầu \(\left( S \right)\), gọi \(\left( P \right)\) là … [Đọc thêm...] vềTừ \(A\) kẻ các tiếp tuyến đến mặt cầu \(\left( S \right)\), gọi \(\left( P \right)\) là mặt phẳng chứa các tiếp điểm, biết \(\left( P \right)\) luôn đi qua một đường thẳng \(d\) cố định. Phương trình đường thẳng \(d\) là:

Trong không gian với hệ tọa độ \(Oxyz\) cho điểm \(A\left( {1\,;2\,;3} \right)\) và đường thẳng \(d:\frac{{x – 2}}{2} = \frac{{y + 2}}{1} = \frac{{z – 3}}{1}\). Tìm tọa độ điểm \(A’\) đối xứng với điểm \(A\) qua đường thẳng \(d\).

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:

Trong không gian với hệ tọa độ \(Oxyz\) cho điểm \(A\left( {1\,;2\,;3} \right)\) và đường thẳng \(d:\frac{{x - 2}}{2} = \frac{{y + 2}}{1} = \frac{{z - 3}}{1}\). Tìm tọa độ điểm \(A'\) đối xứng với điểm \(A\) qua đường thẳng \(d\). A. \(\left( {\frac{8}{3}; - \frac{5}{3};\frac{{10}}{3}} \right)\). B. \(\left( {\frac{8}{3};\frac{5}{3};\frac{{10}}{3}} \right)\). C. \(\left( … [Đọc thêm...] vềTrong không gian với hệ tọa độ \(Oxyz\) cho điểm \(A\left( {1\,;2\,;3} \right)\) và đường thẳng \(d:\frac{{x – 2}}{2} = \frac{{y + 2}}{1} = \frac{{z – 3}}{1}\). Tìm tọa độ điểm \(A’\) đối xứng với điểm \(A\) qua đường thẳng \(d\).

Trong không gian với hệ trục \(Oxyz,\)cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} – 2x – 4y + 6z – 13 = 0\) và đường thẳng \(d:\frac{{x + 1}}{1} = \frac{{y + 2}}{1} = \frac{{z – 1}}{1}\).

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:

… [Đọc thêm...] vềTrong không gian với hệ trục \(Oxyz,\)cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} – 2x – 4y + 6z – 13 = 0\) và đường thẳng \(d:\frac{{x + 1}}{1} = \frac{{y + 2}}{1} = \frac{{z – 1}}{1}\).

Trong không gian  cho mặt cầu \({x^2} + {y^2} + {z^2} = 9\) và điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 2 – 3t\end{array} \right.\). Ba điểm \(A\), \(B\), \(C\) phân biệt cùng thuộc mặt cầu sao cho \(MA\), \(MB\), \(MC\) là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng \(\left( {ABC} \right)\) đi qua \(D\left( {1;1;2} \right)\). Tổng \(T = x_0^2 + y_0^2 + z_0^2\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:,

Trong không gian cho mặt cầu \({x^2} + {y^2} + {z^2} = 9\) và điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 2 - 3t\end{array} \right.\). Ba điểm \(A\), \(B\), \(C\) phân biệt cùng thuộc mặt cầu sao cho \(MA\), \(MB\), \(MC\) là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng \(\left( {ABC} \right)\) đi qua \(D\left( … [Đọc thêm...] vềTrong không gian  cho mặt cầu \({x^2} + {y^2} + {z^2} = 9\) và điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) thuộc \(d:\left\{ \begin{array}{l}x = 1 + t\\y = 1 + 2t\\z = 2 – 3t\end{array} \right.\). Ba điểm \(A\), \(B\), \(C\) phân biệt cùng thuộc mặt cầu sao cho \(MA\), \(MB\), \(MC\) là tiếp tuyến của mặt cầu. Biết rằng mặt phẳng \(\left( {ABC} \right)\) đi qua \(D\left( {1;1;2} \right)\). Tổng \(T = x_0^2 + y_0^2 + z_0^2\) bằng

tập hợp các điểm thỏa mãn \(\left| x \right| + \left| y \right| + \left| z \right| \le 2\) và \(\left| {x – 2} \right| + \left| y \right| + \left| z \right| \le 2\) là một khối đa diện có thể tích bằng

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:,

Trong không gian Oxyz, tập hợp các điểm thỏa mãn \(\left| x \right| + \left| y \right| + \left| z \right| \le 2\) và \(\left| {x - 2} \right| + \left| y \right| + \left| z \right| \le 2\) là một khối đa diện có thể tích bằng: A. \(3 \)      B. \( 2\)  C. \(\frac{8}{3}\)   … [Đọc thêm...] vềtập hợp các điểm thỏa mãn \(\left| x \right| + \left| y \right| + \left| z \right| \le 2\) và \(\left| {x – 2} \right| + \left| y \right| + \left| z \right| \le 2\) là một khối đa diện có thể tích bằng

Trong không gian \(Oxyz\), cho \(\overrightarrow u = 2\overrightarrow j + \overrightarrow k \). Toạ độ của \(2\overrightarrow u \) là

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:

Câu hỏi: Trong không gian \(Oxyz\), cho \(\overrightarrow u = 2\overrightarrow j + \overrightarrow k \). Toạ độ của \(2\overrightarrow u \) là A. \(\left( {4;0;2} \right)\). B. \(\left( {4;2;0} \right)\). C. \(\left( {0;4;2} \right)\). D\(\left( {0;2;1} \right)\). Lời giải Ta có \(\overrightarrow u = 2\overrightarrow j + \overrightarrow k \Rightarrow … [Đọc thêm...] về

Trong không gian \(Oxyz\), cho \(\overrightarrow u = 2\overrightarrow j + \overrightarrow k \). Toạ độ của \(2\overrightarrow u \) là

Cho mặt cầu \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 3} \right)^2} = 4\) và điểm \(A \in \left( S \right)\). Gọi \(B\left( {a;b;c} \right)\) là điểm thỏa mãn \(\overrightarrow {AB} \) cùng phương với \(\overrightarrow u = \left( {1; – 1;2} \right)\) và \(2a – b + 3c + 5 = 0\). Độ dài đoạn thẳng \(AB\) lớn nhất bằng

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:

Câu hỏi: Cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 4\) và điểm \(A \in \left( S \right)\). Gọi \(B\left( {a;b;c} \right)\) là điểm thỏa mãn \(\overrightarrow {AB} \) cùng phương với \(\overrightarrow u = \left( {1; - 1;2} \right)\) và \(2a - b + 3c + 5 = 0\). Độ dài đoạn thẳng \(AB\) lớn nhất … [Đọc thêm...] về

Cho mặt cầu \(\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z – 3} \right)^2} = 4\) và điểm \(A \in \left( S \right)\). Gọi \(B\left( {a;b;c} \right)\) là điểm thỏa mãn \(\overrightarrow {AB} \) cùng phương với \(\overrightarrow u = \left( {1; – 1;2} \right)\) và \(2a – b + 3c + 5 = 0\). Độ dài đoạn thẳng \(AB\) lớn nhất bằng

Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):2x + y + z + 1 = 0\) và đường thẳng \(d:\frac{{x – 1}}{2} = \frac{{y – 2}}{{ – 1}} = \frac{{z – 3}}{1}\). Phương trình tham số của đường thẳng \(\Delta \) đi qua \(A\left( { – 3;4;1} \right)\), vuông góc với \(d\) và nằm trong \(\left( P \right)\) là:

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:

Câu hỏi: Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):2x + y + z + 1 = 0\) và đường thẳng \(d:\frac{{x - 1}}{2} = \frac{{y - 2}}{{ - 1}} = \frac{{z - 3}}{1}\). Phương trình tham số của đường thẳng \(\Delta \) đi qua \(A\left( { - 3;4;1} \right)\), vuông góc với \(d\) và nằm trong \(\left( P \right)\) là: A. \(\Delta :\left\{ … [Đọc thêm...] về

Trong không gian với hệ trục tọa độ \(Oxyz\), cho mặt phẳng \(\left( P \right):2x + y + z + 1 = 0\) và đường thẳng \(d:\frac{{x – 1}}{2} = \frac{{y – 2}}{{ – 1}} = \frac{{z – 3}}{1}\). Phương trình tham số của đường thẳng \(\Delta \) đi qua \(A\left( { – 3;4;1} \right)\), vuông góc với \(d\) và nằm trong \(\left( P \right)\) là:

Trong không gian \({\rm{Oxyz}}\), cho hai mặt phẳng\(\left( P \right):2x – y + 3z – 3 = 0;\,\left( Q \right):x – y + 2z – 3 = 0\). Phương trình mặt phẳng chứa giao tuyến của\(\left( P \right),\,\left( Q \right)\) và cắt tia \(Ox,Oy,Oz\) tại các điểm \(A,B,C\) sao cho \({V_{OABC}} = 6\) đi qua điểm nào sau đây

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:

Câu hỏi: Trong không gian \({\rm{Oxyz}}\), cho hai mặt phẳng\(\left( P \right):2x - y + 3z - 3 = 0;\,\left( Q \right):x - y + 2z - 3 = 0\). Phương trình mặt phẳng chứa giao tuyến của\(\left( P \right),\,\left( Q \right)\) và cắt tia \(Ox,Oy,Oz\) tại các điểm \(A,B,C\) sao cho \({V_{OABC}} = 6\) đi qua điểm nào sau đây A. \(A\left( {1;1;1} \right)\). B. \(B\left( … [Đọc thêm...] về

Trong không gian \({\rm{Oxyz}}\), cho hai mặt phẳng\(\left( P \right):2x – y + 3z – 3 = 0;\,\left( Q \right):x – y + 2z – 3 = 0\). Phương trình mặt phẳng chứa giao tuyến của\(\left( P \right),\,\left( Q \right)\) và cắt tia \(Ox,Oy,Oz\) tại các điểm \(A,B,C\) sao cho \({V_{OABC}} = 6\) đi qua điểm nào sau đây

Trong không gian \(Oxyz\), tìm tất cả các giá trị của \(m\) để hai vecto \(\overrightarrow a = \left( {1;1; – 3} \right)\) và \(\overrightarrow b = \left( {1;{m^2}; – 3} \right)\) bằng nhau?

Ngày Thuộc chủ đề:Trắc nghiệm Hình học OXYZ Tag với:

Câu hỏi: Trong không gian \(Oxyz\), tìm tất cả các giá trị của \(m\) để hai vecto \(\overrightarrow a = \left( {1;1; - 3} \right)\) và \(\overrightarrow b = \left( {1;{m^2}; - 3} \right)\) bằng nhau? A. \(m = 2\). B. \(m = 1\). C. \(m = - 1\). D. \(m = \pm 1\). Lời giải Ta có \(\overrightarrow a = \overrightarrow b \Leftrightarrow \left\{ … [Đọc thêm...] về

Trong không gian \(Oxyz\), tìm tất cả các giá trị của \(m\) để hai vecto \(\overrightarrow a = \left( {1;1; – 3} \right)\) và \(\overrightarrow b = \left( {1;{m^2}; – 3} \right)\) bằng nhau?