Trong không gian với hệ trục \(Oxyz,\)cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} – 2x – 4y + 6z – 13 = 0\) và đường thẳng \(d:\frac{{x + 1}}{1} = \frac{{y + 2}}{1} = \frac{{z – 1}}{1}\).

Trong không gian với hệ trục \(Oxyz,\)cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} – 2x – 4y + 6z – 13 = 0\) và đường thẳng \(d:\frac{{x + 1}}{1} = \frac{{y + 2}}{1} = \frac{{z – 1}}{1}\). Điểm \(M\left( {a;b;c} \right)\,,\left( {a > 0} \right)\) nằm trên đường thẳng \(d\) sao cho từ \(M\) kẻ được ba tiếp tuyến \(MA,\,\,MB,\,\,MC\)đến mặt cầu \(\left( S \right)\) (\(A,\,\,B,\,\,C\) là các tiếp điểm) và \(\widehat {AMB} = {60^0}\), \(\widehat {BMC} = {60^0}\), \(\widehat {CMA} = {120^0}\). Tính \({a^3} + {b^3} + {c^3}\).
A. \({a^3} + {b^3} + {c^3} = \frac{{173}}{9}\).      B. \({a^3} + {b^3} + {c^3} = \frac{{112}}{9}\).  C. \({a^3} + {b^3} + {c^3} =  – 8\).                             D. \({a^3} + {b^3} + {c^3} = \frac{{23}}{9}\).
Lời giải

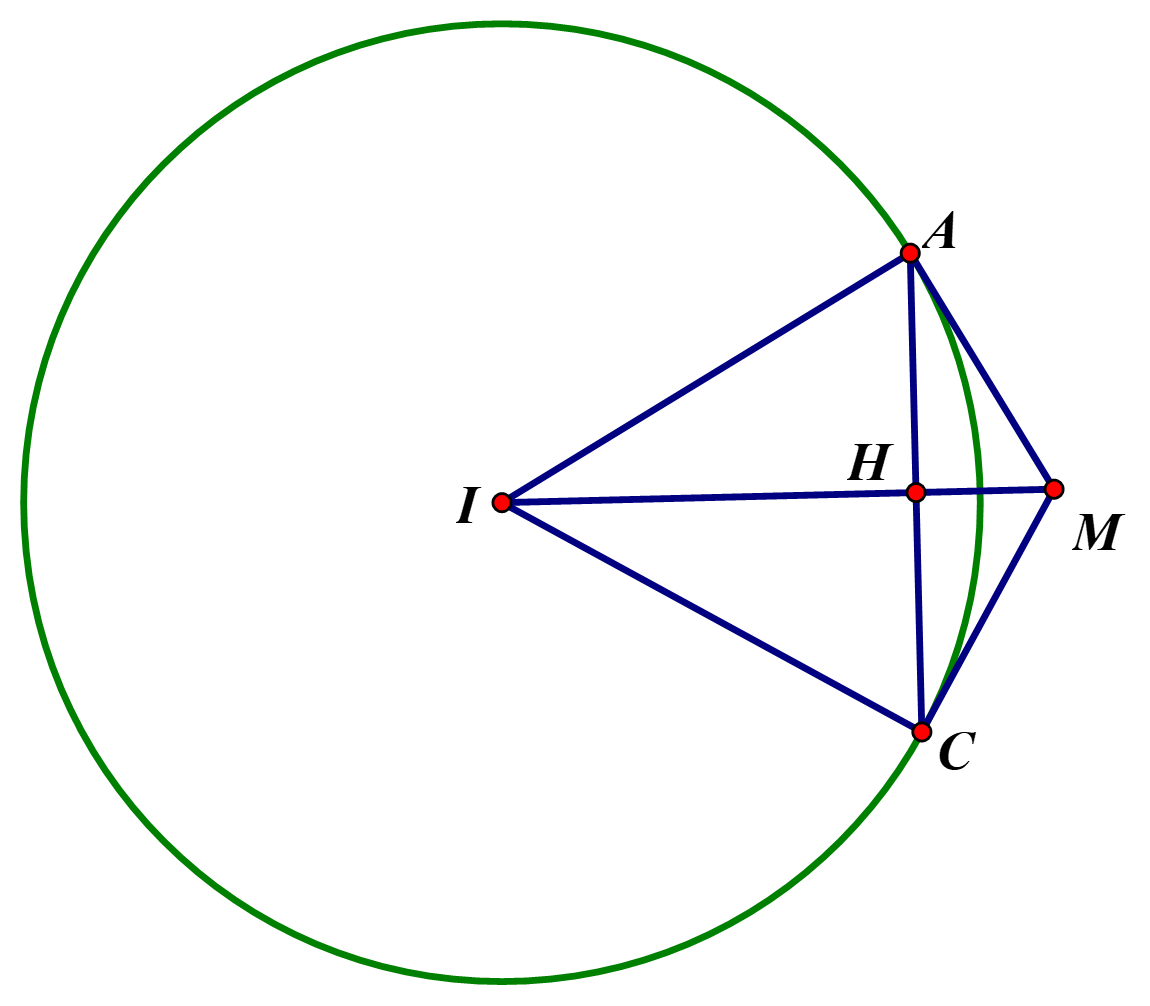
Mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2; – 3} \right)\) và bán kính \(R = \sqrt {{1^2} + {2^2} + {{\left( { – 3} \right)}^2} + 13}  = 3\sqrt 3 \)
Gọi \(\left( C \right)\) là đường tròn giao tuyến của mặt phẳng \(\left( {ABC} \right)\) và mặt cầu \(\left( S \right)\).
Đặt \(MA = MB = MC = x\) khi đó \(AB = x;BC = x\sqrt 2 ;CA = x\sqrt 3 \) do đó tam giác \(ABC\) vuông tại \(B\) nên trung điểm \(H\)của \(AC\) là tâm đường tròn \(\left( C \right)\) và \(H,\,\,I,\,\,M\) thẳng hàng.
Vì \(\widehat {AMC} = {120^0}\) nên tam giác \(AIC\) đều do đó \(x\sqrt 3  = R\) \( \Leftrightarrow x = 3\) suy ra \(IM = 2AM = 2x = 6\).
Lại có \(M \in d\) nên \(M\left( { – 1 + t; – 2 + t;1 + t} \right),\left( {t > 1} \right)\) mà \(IM = 6\) nên \({\left( {t – 2} \right)^2} + {\left( {t – 4} \right)^2} + {\left( {t + 4} \right)^2} = 36\) \( \Leftrightarrow 3{t^2} – 4t = 0\)\( \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = \frac{4}{3}\end{array} \right.\).
Mà a > 0 nên \(t = \frac{4}{3}\) suy ra \(H\left( {\frac{1}{3}; – \frac{2}{3};\frac{7}{3}} \right)\) nên \({a^3} + {b^3} + {c^3} = \frac{{112}}{9}\).