Cho hàm số $y=x\ln x$. Đặt $M=\max\limits_{\left[ \dfrac{1}{{{e}^{2}}};e \right]} y$, $m=\min\limits_{\left[ \dfrac{1}{{{e}^{2}}};e \right]} y$. Tính giá trị $M.m$ bằng ……Đáp án: -1Lời giải: Hàm số đã cho liên tục và xác định trên đoạn $\left[ \dfrac{1}{{{e}^{2}}};e \right]$ Ta có ${y}'=\ln x+1$. Xét ${y}'=0\Leftrightarrow \ln x+1=0\Leftrightarrow x=\dfrac{1}{e}\in \left[ … [Đọc thêm...] vềCho hàm số $y=x\ln x$. Đặt $M=\max\limits_{\left[ \dfrac{1}{{{e}^{2}}};e \right]} y$, $m=\min\limits_{\left[ \dfrac{1}{{{e}^{2}}};e \right]} y$
Toán thực tế MAX - MIN
Một doanh nghiệp dự kiến lợi nhuận khi sản xuất $x$ sản phẩm ( $0\le x\le 300$ ) được cho bởi hàm số $y=-{{x}^{3}}+300{{x}^{2}}$ (đơn vị: đồng) và được minh họa bằng đồ thị ở hình bên dưới
Một doanh nghiệp dự kiến lợi nhuận khi sản xuất $x$ sản phẩm ( $0\le x\le 300$ ) được cho bởi hàm số $y=-{{x}^{3}}+300{{x}^{2}}$ (đơn vị: đồng) và được minh họa bằng đồ thị ở hình bên dưới. Cần sản xuất bao nhiêu sản phẩm để doanh nghiệp thu được lợi nhuận cao nhất?Đáp án: 200Lời giải: Dựa vào đồ thị ta thấy hàm số có giá trị lớn nhất bằng $4000000$ khi $x=200$. Do đó cần sản … [Đọc thêm...] vềMột doanh nghiệp dự kiến lợi nhuận khi sản xuất $x$ sản phẩm ( $0\le x\le 300$ ) được cho bởi hàm số $y=-{{x}^{3}}+300{{x}^{2}}$ (đơn vị: đồng) và được minh họa bằng đồ thị ở hình bên dưới
Đồ thị của hàm số $y=f(x)$ có dạng như đường cong trong hình vẽ bên dưới
Đồ thị của hàm số $y=f(x)$ có dạng như đường cong trong hình vẽ bên dưới. Gọi $M$ là giá trị lớn nhất, $m$ là giá trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn $[-1;1]$. Tính $P=M-2m$. Đáp án: 5Lời giải: Dựa vào hình vẽ ta thấy $M=\max\limits_{[-1;1]}f(x)=f(-1)=3$, $m=\lim\limits_{[-1;1]}f(x)=f(1)=-1$. Vậy $P=M-2m=3-2\cdot (-1)=5$. … [Đọc thêm...] vềĐồ thị của hàm số $y=f(x)$ có dạng như đường cong trong hình vẽ bên dưới
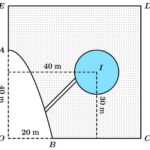
Một cái ao có hình ABCDE (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 10m, người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hỏi độ dài ngắn nhất l (đơn vị mét) của cây cầu là bao nhiêu (làm tròn đến chữ số hàng phần chục), biết:
- Hai bờ AE và BC nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại điểm O; - Bờ AB là một phần của một parabol có đỉnh là điểm A và có trục đối xứng là đường thẳng OA ; - Độ dài đoạn OA và OB lần lượt là 40m và 20m; - Tâm I của mảnh vườn cách đường … [Đọc thêm...] vềMột cái ao có hình ABCDE (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 10m, người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hỏi độ dài ngắn nhất l (đơn vị mét) của cây cầu là bao nhiêu (làm tròn đến chữ số hàng phần chục), biết:
Đề: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là \(f'\left( t \right) = 4{t^3} – \frac{{{t^2}}}{2}\) (người). Nếu xem \(f'\left( t \right)\) là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ mấy?
Câu hỏi: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là \(f'\left( t \right) = 4{t^3} - \frac{{{t^2}}}{2}\) (người). Nếu xem \(f'\left( t \right)\) là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ … [Đọc thêm...] vềĐề: Sau khi phát hiện một bệnh dịch, các chuyên gia y tế ước tính số người nhiễm bệnh kể từ ngày xuất hiện bệnh nhân đầu tiên đến ngày thứ t là \(f'\left( t \right) = 4{t^3} – \frac{{{t^2}}}{2}\) (người). Nếu xem \(f'\left( t \right)\) là tốc độ truyền bệnh (người/ngày) tại thời điểm t. Tốc độ truyền bệnh sẽ lớn nhất vào ngày thứ mấy?
Đề: Người ta cần xây một hồ nước với dạng khối hộp chữ nhật không nắp có thể tích bằng \(\frac{{288}}{5}{m^3}.\) Đáy hồ là hình chữ nhật có chiều dài gấp rưỡi chiều rộng. Giá thuê nhân công để xây hồ là 500 000 đồng/\({m^2}.\) Nếu kích thước của hồ nước được tính toán để chi phí thuê nhân công là ít nhất thì chi phí đó là bao nhiêu?
Câu hỏi: Người ta cần xây một hồ nước với dạng khối hộp chữ nhật không nắp có thể tích bằng \(\frac{{288}}{5}{m^3}.\) Đáy hồ là hình chữ nhật có chiều dài gấp rưỡi chiều rộng. Giá thuê nhân công để xây hồ là 500 000 đồng/\({m^2}.\) Nếu kích thước của hồ nước được tính toán để chi phí thuê nhân công là ít nhất thì chi phí đó là bao nhiêu? A.28 (triệu … [Đọc thêm...] vềĐề: Người ta cần xây một hồ nước với dạng khối hộp chữ nhật không nắp có thể tích bằng \(\frac{{288}}{5}{m^3}.\) Đáy hồ là hình chữ nhật có chiều dài gấp rưỡi chiều rộng. Giá thuê nhân công để xây hồ là 500 000 đồng/\({m^2}.\) Nếu kích thước của hồ nước được tính toán để chi phí thuê nhân công là ít nhất thì chi phí đó là bao nhiêu?
Đề: Một chất điểm chuyển động theo quy luật (t tính theo giây). Vận tốc của chất điểm đạt giá trị nhỏ nhất tại thời điểm nào?
Câu hỏi: Một chất điểm chuyển động theo quy luật (t tính theo giây). Vận tốc của chất điểm đạt giá trị nhỏ nhất tại thời điểm nào? A.t=1 giây B.t=3 giây C.t=5 giây D.t=16 giây Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới. Có vấn đề về lời giải xin các bạn để lại phản hồi … [Đọc thêm...] vềĐề: Một chất điểm chuyển động theo quy luật (t tính theo giây). Vận tốc của chất điểm đạt giá trị nhỏ nhất tại thời điểm nào?
Đề: Một khối gỗ hình trụ có chiều cao 2m người ta xẻ bớt phần vỏ của khối gỗ đó theo bốn mặt phẳng song song với trục để tạo thành một khối gỗ hình hộp chữ nhật có thể tích lớn nhất bằng 1m3. Tính đường kính của khối gỗ hình trụ đã cho.
Câu hỏi: Một khối gỗ hình trụ có chiều cao 2m người ta xẻ bớt phần vỏ của khối gỗ đó theo bốn mặt phẳng song song với trục để tạo thành một khối gỗ hình hộp chữ nhật có thể tích lớn nhất bằng 1m3. Tính đường kính của khối gỗ hình trụ đã cho. A.\(100cm.\) B.\(60cm.\) C.\(120cm.\) D.\(50cm.\) … [Đọc thêm...] vềĐề: Một khối gỗ hình trụ có chiều cao 2m người ta xẻ bớt phần vỏ của khối gỗ đó theo bốn mặt phẳng song song với trục để tạo thành một khối gỗ hình hộp chữ nhật có thể tích lớn nhất bằng 1m3. Tính đường kính của khối gỗ hình trụ đã cho.
Đề: Một vật chuyển động theo quy luật \(s = 9{t^2} – {t^3},\) với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 5 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
Câu hỏi: Một vật chuyển động theo quy luật \(s = 9{t^2} - {t^3},\) với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 5 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu? A.27 m/s. B.15 … [Đọc thêm...] vềĐề: Một vật chuyển động theo quy luật \(s = 9{t^2} – {t^3},\) với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 5 giây, kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
Đề: Một ngọn hải đăng được đặt tại vị trí \(A\) trên mặt biển cách bờ biển một khoảng \(AB = 5km\) . Trên bờ biển có một cái kho ở cách \(B\) \(7\) km. Người canh hải đăng có thể chèo đò đến điểm \(M\) trên bờ biển với vận tốc \(4km/h\) rồi đi bộ đến \(C\) với vận tốc \(6km/h\) . Vị trí của điểm \(M\) cách \(B\) một khoảng bằng bao nhiêu để người đó đi đến kho \(C\) ít tốn thời gian nhất.
Câu hỏi: Một ngọn hải đăng được đặt tại vị trí \(A\) trên mặt biển cách bờ biển một khoảng \(AB = 5km\) . Trên bờ biển có một cái kho ở cách \(B\) \(7\) km. Người canh hải đăng có thể chèo đò đến điểm \(M\) trên bờ biển với vận tốc \(4km/h\) rồi đi bộ đến \(C\) với vận tốc \(6km/h\) . Vị trí của điểm \(M\) cách \(B\) một khoảng bằng bao nhiêu để người đó đi đến kho … [Đọc thêm...] vềĐề: Một ngọn hải đăng được đặt tại vị trí \(A\) trên mặt biển cách bờ biển một khoảng \(AB = 5km\) . Trên bờ biển có một cái kho ở cách \(B\) \(7\) km. Người canh hải đăng có thể chèo đò đến điểm \(M\) trên bờ biển với vận tốc \(4km/h\) rồi đi bộ đến \(C\) với vận tốc \(6km/h\) . Vị trí của điểm \(M\) cách \(B\) một khoảng bằng bao nhiêu để người đó đi đến kho \(C\) ít tốn thời gian nhất.