Một doanh nghiệp dự kiến lợi nhuận khi sản xuất $x$ sản phẩm ( $0\le x\le 300$ ) được cho bởi hàm số $y=-{{x}^{3}}+300{{x}^{2}}$ (đơn vị: đồng) và được minh họa bằng đồ thị ở hình bên dưới

Một doanh nghiệp dự kiến lợi nhuận khi sản xuất $x$ sản phẩm ( $0\le x\le 300$ ) được cho bởi hàm số $y=-{{x}^{3}}+300{{x}^{2}}$ (đơn vị: đồng) và được minh họa bằng đồ thị ở hình bên dưới.

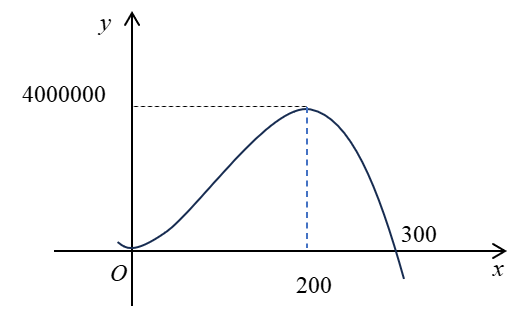
Cần sản xuất bao nhiêu sản phẩm để doanh nghiệp thu được lợi nhuận cao nhất?
Đáp án: 200

Lời giải: Dựa vào đồ thị ta thấy hàm số có giá trị lớn nhất bằng $4000000$ khi $x=200$.
Do đó cần sản suất $200$ sản phẩm thì doanh nghiệp thu được lợi nhuận cao nhất.