Quan he vuong goc

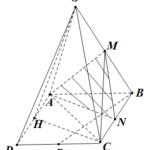
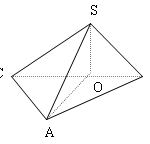
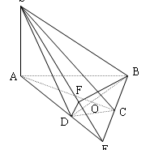
Đề bài: Cho hình chóp tứ giác $S.ABCD$ đáy là hình vuông, cạnh $a$. Mặt bên $SAD$ là tam giác đều và ở trong mặt phẳng vuông góc với đáy. Gọi $M,N,P$ lần lượt là trung điểm $SB, BC, CD$ Chứng minh $AM \bot BP$ Lời giải Gọi $H$ là trung điểm của $AD$ do $SAD$ là tam giác đều , nên $SH \bot AD$.Vì $(SAD) \bot (ABCD)\Rightarrow SH \bot (ABCD)\Rightarrow SH \bot BP … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác $S.ABCD$ đáy là hình vuông, cạnh $a$. Mặt bên $SAD$ là tam giác đều và ở trong mặt phẳng vuông góc với đáy. Gọi $M,N,P$ lần lượt là trung điểm $SB, BC, CD$ Chứng minh $AM \bot BP$

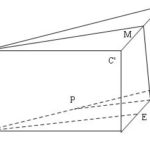
Đề bài: cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có cạnh đáy bằng $2a$ và chiều cao $a$$1.$ Dựng thiết diện của lăng trụ tạo bởi mặt phẳng đi qua $B'$ và vuông góc với cạnh $A'C$$2.$ Tính diện tích thiết diện nói trên Lời giải $1.$ Gọi $M, P, E$ là trung điểm $A’C ', AB,AC$. Gọi $N$ là trung điểm $AE$. Ta sẽ chứng tỏ $M’MNP$ là thiết diện … [Đọc thêm...] vềĐề bài: cho hình lăng trụ tam giác đều $ABC.A'B'C'$ có cạnh đáy bằng $2a$ và chiều cao $a$$1.$ Dựng thiết diện của lăng trụ tạo bởi mặt phẳng đi qua $B'$ và vuông góc với cạnh $A'C$$2.$ Tính diện tích thiết diện nói trên

Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ lần lượt là trung điểm của $AE,BC$.1) Chứng minh $MN\bot BD$.2) Tính theo $a$ khoảng cách giữa hai đường thẳng $MN,AC$. Lời giải a. Gọi O là tâm của ABCDI là trung điểm của ABIN giao BO tại K$\begin{cases}IN//AC \\ BD\bot … [Đọc thêm...] vềĐề bài: Cho hình chóp tứ giác đều $S.ABCD$ cạnh đáy bằng $a$. Gọi $E$ là điểm đối xứng của $D$ qua trung điểm của $SA$. Gọi $M,N$ lần lượt là trung điểm của $AE,BC$.1) Chứng minh $MN\bot BD$.2) Tính theo $a$ khoảng cách giữa hai đường thẳng $MN,AC$.

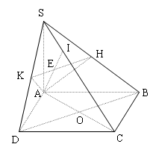
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,SA$ vuông góc với mặt phẳng $(ABCD)$.Gọi $H,I,K$ lần lượt là hình chiếu vuông góc của điểm $A$ trên $SB,SC,SD$$a.$ Chứng minh rằng $BC\bot (SAB),CD\bot (SAD)$$b.$ Chứng minh rằng $(SAC)$ là mặt phẳng trung trực của đoạn $BD$$c.$ Chứng minh rằng $AH,AK$ cùng vuông góc với $SC$. Từ đó suy ra ba đường thẳng … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,SA$ vuông góc với mặt phẳng $(ABCD)$.Gọi $H,I,K$ lần lượt là hình chiếu vuông góc của điểm $A$ trên $SB,SC,SD$$a.$ Chứng minh rằng $BC\bot (SAB),CD\bot (SAD)$$b.$ Chứng minh rằng $(SAC)$ là mặt phẳng trung trực của đoạn $BD$$c.$ Chứng minh rằng $AH,AK$ cùng vuông góc với $SC$. Từ đó suy ra ba đường thẳng $AH,AI,AK$ cùng chứa trong một mặt phẳng.$d.$ Chứng minh rằng $(SAC)$ là mặt phẳng trung trực của đoạn $HK$. Từ đó suy ra $HK\bot AI$$e.$ Tính diện tích tứ giác $AHIK$ biết $SA=AB=a$

Đề bài: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $A,BC=a,SA=SB=SC=\frac{a\sqrt{3} }{2} $$a.$ Tính khoảng cách từ $S$ tới mặt phẳng $(ABC)$$b.$ Tính góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$ Lời giải $a.$ Gọi $O$ là trung điểm của $BC$ suy ra $O$ là tâm đường tròn ngoại tiếp $\Delta ABC$Ngoài ra theo giả thiết ta có : $SA=SB=SC$ nên  $SO$ là trục … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$ đáy $ABC$ là tam giác vuông tại $A,BC=a,SA=SB=SC=\frac{a\sqrt{3} }{2} $$a.$ Tính khoảng cách từ $S$ tới mặt phẳng $(ABC)$$b.$ Tính góc giữa đường thẳng $SA$ và mặt phẳng $(ABC)$

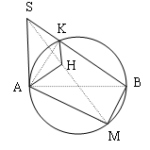
Đề bài: Trong mặt phẳng $(\alpha)$ cho đường tròn $(C)$ đường kính $AB,SA$ vuông góc với $(\alpha)$.Gọi $M$ là một điểm di động trên $(C),H$ là hình chiếu vuông góc của điểm $A$ trên mặt phẳng $(SBM)$.Tìm tập hợp các điểm $H$ Lời giải Nhận thấy mặt phẳng $SBM$ chứa đường thẳng $SB$ cố định.Ta đi dựng mặt phẳng qua $A$ và vuông góc với $SB$ bằng cách :- Trong $(SAB)$ … [Đọc thêm...] vềĐề bài: Trong mặt phẳng $(\alpha)$ cho đường tròn $(C)$ đường kính $AB,SA$ vuông góc với $(\alpha)$.Gọi $M$ là một điểm di động trên $(C),H$ là hình chiếu vuông góc của điểm $A$ trên mặt phẳng $(SBM)$.Tìm tập hợp các điểm $H$

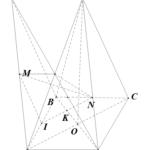
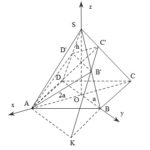
Đề bài: Hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi với các đường chéo $AC=4a, BD=2a$, chúng cắt nhau tại $O$. Đường cao hình chóp $SO=h$. Mặt phẳng $(\alpha )$ qua $A$, vuông góc với $SC$ và cắt $SB, SC, SD$ lần lượt tại $B',C',D'$a) Xác định $h$ để $\Delta B'C'D'$ đềub) Tính bán kính $r$ của mặt cầu nội tiếp hình chóp theo $a$ và $h$ … [Đọc thêm...] vềĐề bài: Hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi với các đường chéo $AC=4a, BD=2a$, chúng cắt nhau tại $O$. Đường cao hình chóp $SO=h$. Mặt phẳng $(\alpha )$ qua $A$, vuông góc với $SC$ và cắt $SB, SC, SD$ lần lượt tại $B',C',D'$a) Xác định $h$ để $\Delta B'C'D'$ đềub) Tính bán kính $r$ của mặt cầu nội tiếp hình chóp theo $a$ và $h$

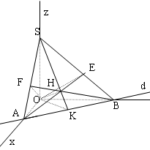
Đề bài: Trong mặt phẳng $\alpha$ cho góc vuông $xOy,d$ là đường thẳng cố định trong $\alpha,d$ cắt $Ox,Oy$ lần lượt tại $A,B$.Gọi $Oz$ là tia vuông góc với $\alpha,S$ là một điểm trên $Oz$.Gọi $AE,BF$ là đường cao của $\Delta SAB$$a.$ Cho góc $xOy$ cố định,$S$ di động trên tia $Oz$.Tìm tập hợp các điểm $E,F$$b.$ Cho $d$ cố định, góc $xOy$ xoay quanh $O$.Chứng minh rằng trực tâm … [Đọc thêm...] vềĐề bài: Trong mặt phẳng $\alpha$ cho góc vuông $xOy,d$ là đường thẳng cố định trong $\alpha,d$ cắt $Ox,Oy$ lần lượt tại $A,B$.Gọi $Oz$ là tia vuông góc với $\alpha,S$ là một điểm trên $Oz$.Gọi $AE,BF$ là đường cao của $\Delta SAB$$a.$ Cho góc $xOy$ cố định,$S$ di động trên tia $Oz$.Tìm tập hợp các điểm $E,F$$b.$ Cho $d$ cố định, góc $xOy$ xoay quanh $O$.Chứng minh rằng trực tâm của $\Delta SAB$ cố định.Tìm tập hợp các điểm $E,F$

Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là nửa lục giác đều nội tiếp đường tròn đường kính $AB=2a,SA=a\sqrt{3} $ và vuông góc với mặt phẳng $(ABCD)$$a.$ Tính góc giữa hai mặt phẳng $(SAD)$ và $(SBC)$$b.$ Tính góc giữa hai mặt phẳng $(SBC)$ và $(SCD)$ Lời giải $a.$ Ta có thể lựa chọn một trong hai cách trình bày sau :Cách $1:$ (Dựng góc dựa trên giao tuyến) : … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là nửa lục giác đều nội tiếp đường tròn đường kính $AB=2a,SA=a\sqrt{3} $ và vuông góc với mặt phẳng $(ABCD)$$a.$ Tính góc giữa hai mặt phẳng $(SAD)$ và $(SBC)$$b.$ Tính góc giữa hai mặt phẳng $(SBC)$ và $(SCD)$