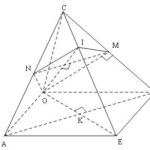
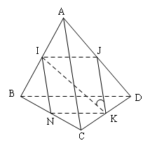
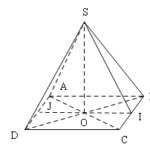
Đề bài: Cho tứ diện $OABC$ có cạnh $OA, OB, OC$ đôi một vuông góc với nhau và $OA = OB = OC = a$. Kí hiệu $K, M, N$ lần lượt là trung điểm của các cạnh $AB, BC, CA$. Gọi $E$ là điểm đối xứng của $O$ qua $K$ và $I$ là giao […]
Quan he vuong goc
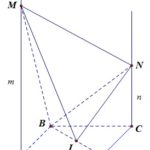
Đề bài: Cho hình vuông $ABCD$ cạnh $a$, tâm $I$ ($A$ đối diện với $C$). Các nửa đường thẳng $Ax, Cy$ vuông góc với mặt phẳng $(ABCD)$ và ở cùng một phía đối với mặt phẳng đó. Cho điểm $M$ không trùng với $A$ trên $Ax$, cho điểm $N$ không trùng với $C$ trên $Cy$. Đặt $AM = m, CN = n$.$1$. Tính thể tích của hình chóp $B.AMNC$ (đỉnh $B$, đáy $AMNC$).$2$. Tính $MN$ theo $a, m, n$ và tìm điều kiện đối với $a, m, n$ để góc \(\widehat {MIN}\) là góc vuông.
Đề bài: Cho hình vuông $ABCD$ cạnh $a$, tâm $I$ ($A$ đối diện với $C$). Các nửa đường thẳng $Ax, Cy$ vuông góc với mặt phẳng $(ABCD)$ và ở cùng một phía đối với mặt phẳng đó. Cho điểm $M$ không trùng với $A$ trên $Ax$, cho điểm $N$ không trùng với $C$ trên $Cy$. […]
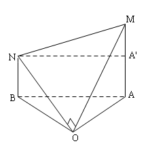
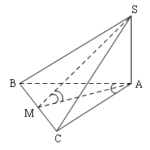
Đề bài: Trong mặt phẳng $(P)$ cho tam giác $OAB$, cân tại đỉnh $O,OA=a$ và cạnh đáy $AB=a\sqrt{3} $.Trên các đường thẳng $Ax\bot (P),By\bot (P)$ với $Ax,By$ nằm cùng phía đối với mặt phẳng $(P)$, ta lấy theo thứ tự, hai điểm $M,N$ sao cho $AM=a,BN=\frac{a}{2} $$a.$ Chứng minh tam giác $OMN$ vuông$b.$ Tính góc hợp bởi mặt phẳng $(OMN),(P)$
Đề bài: Trong mặt phẳng $(P)$ cho tam giác $OAB$, cân tại đỉnh $O,OA=a$ và cạnh đáy $AB=a\sqrt{3} $.Trên các đường thẳng $Ax\bot (P),By\bot (P)$ với $Ax,By$ nằm cùng phía đối với mặt phẳng $(P)$, ta lấy theo thứ tự, hai điểm $M,N$ sao cho $AM=a,BN=\frac{a}{2} $$a.$ Chứng minh tam giác $OMN$ vuông$b.$ Tính góc […]
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a; SA$ vuông góc với đáy. Gọi $M,N$ là trung điểm của $AD, SC$. Chứng minh mặt phẳng $(SAC)$ vuông góc với mặt phẳng $(SMB)$.
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{2}, SA=a; SA$ vuông góc với đáy. Gọi $M,N$ là trung điểm của $AD, SC$. Chứng minh mặt phẳng $(SAC)$ vuông góc với mặt phẳng $(SMB)$. Lời giải Giả sử $AC\cap MB=I$.Vì $MA=MD$ và do $AD//BC$,nên theo định lí Talet […]
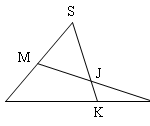
Đề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$
Đề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$ Lời giải cần giải […]
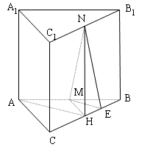
Đề bài: Cho hình lăng trụ đứng $ABC.A_1B_1C_1$ có đáy $ABC$ vuông cân tại $A$.Đoạn nối trung điểm $M$ của $AB$ và trung điểm $N$ của $B_1C_1$ có độ dài bằng $a,MN$ hợp với đáy góc $\alpha $ và mặt bên $(BCC_1B_1)$ góc $\beta $$a.$ Tính các đáy và cạnh bên của lăng trụ theo $a,\alpha $$b.$ chứng minh rằng $cos\alpha =\sqrt{2}sin\beta $
Đề bài: Cho hình lăng trụ đứng $ABC.A_1B_1C_1$ có đáy $ABC$ vuông cân tại $A$.Đoạn nối trung điểm $M$ của $AB$ và trung điểm $N$ của $B_1C_1$ có độ dài bằng $a,MN$ hợp với đáy góc $\alpha $ và mặt bên $(BCC_1B_1)$ góc $\beta $$a.$ Tính các đáy và cạnh bên của lăng trụ theo […]
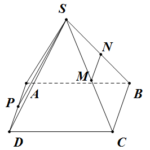
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, tâm $O$.Gọi $M,N$ lần lượt là trung điểm của các cạnh $SA,BC$.Biết rằng góc giữa $MN$ và $(ABCD)$ bằng $60^0$$a.$ Tính $MN,SO$$b.$ Tính góc giữa $MN$ và mặt phẳng $(SBD)$
Đề bài: Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, tâm $O$.Gọi $M,N$ lần lượt là trung điểm của các cạnh $SA,BC$.Biết rằng góc giữa $MN$ và $(ABCD)$ bằng $60^0$$a.$ Tính $MN,SO$$b.$ Tính góc giữa $MN$ và mặt phẳng $(SBD)$ Lời giải $a.$ Gọi $H$ là trung điểm của $OA$ suy […]
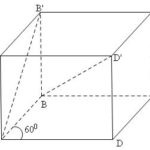
Đề bài: Cho lăng trụ đứng $ABCD.A’B’C’D’$ có đáy $ABCD$ là hình thoi cạnh $a$, góc nhọn $\widehat {BAD} = 60^0$. Biết $\overrightarrow {AB'} \bot \overrightarrow {BD'} $. Tính thể tích lăng trụ trên theo $a$.
Đề bài: Cho lăng trụ đứng $ABCD.A’B’C’D’$ có đáy $ABCD$ là hình thoi cạnh $a$, góc nhọn $\widehat {BAD} = 60^0$. Biết $\overrightarrow {AB'} \bot \overrightarrow {BD'} $. Tính thể tích lăng trụ trên theo $a$. Lời giải Đặt $h=AA’.$ Dễ thấy $\overrightarrow {AB’} =\overrightarrow {AA’}+\overrightarrow {A’B’} $ và $\overrightarrow {BD’} =\overrightarrow {AA’} +\overrightarrow {AD} […]
Đề bài: Cho hình chóp $S.ABCD$ có đáy là $ABCD$ là hình thoi tâm $O$, cạnh $a$ góc $\widehat{A}=60^0 $ và có đường cao $SO=a$$a.$ Tính khoảng cách từ $O$ đến $(SBC)$$b.$ Tính khoảng cách giữa hai đường thẳng $AD,SB$
Đề bài: Cho hình chóp $S.ABCD$ có đáy là $ABCD$ là hình thoi tâm $O$, cạnh $a$ góc $\widehat{A}=60^0 $ và có đường cao $SO=a$$a.$ Tính khoảng cách từ $O$ đến $(SBC)$$b.$ Tính khoảng cách giữa hai đường thẳng $AD,SB$ Lời giải $a.$ Hạ $OI$ vuông góc với $BC$ và kéo dài $OI$ cắt $AD$ […]
Đề bài: Từ một điểm $S$ ngoài mặt phẳng $(P)$ ta kẻ đường thẳng $SA$ vuông góc với mặt phẳng $(P)$ và nối $S$ với hai điểm phân biệt $B,C$ thuộc mặt phẳng $(P)$.Các đường thẳng $SB,SC$ tạo với mặt phẳng $(P)$ các góc $45^0$ và tạo với nhau góc $60^0$$a.$ Chứng minh hai mặt phẳng $(SAB),(SAC)$ vuông góc với nhau$b.$ Tính góc giữa các mặt phẳng $(SBC),(P)$
Đề bài: Từ một điểm $S$ ngoài mặt phẳng $(P)$ ta kẻ đường thẳng $SA$ vuông góc với mặt phẳng $(P)$ và nối $S$ với hai điểm phân biệt $B,C$ thuộc mặt phẳng $(P)$.Các đường thẳng $SB,SC$ tạo với mặt phẳng $(P)$ các góc $45^0$ và tạo với nhau góc $60^0$$a.$ Chứng minh hai mặt […]