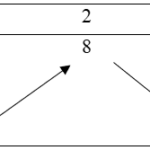
Bài toán gốc Hàm số $y=f(x)$ đạt giá trị nhỏ nhất trên $[-4;1]$ tại điểm nào? Biết hàm số có bảng biến thiên như hình dưới đây A. -4. B. -3. C. 1. D. -14. Lời giải: $y=f(x)=-x^3-6x^2-9x+2$ Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị nhỏ nhất (GTNN) […]
Quiz - Max - Min
Hàm số $y=f(x)$ đạt giá trị lớn nhất trên $[-4;0]$ tại điểm nào? Biết hàm số có bảng biến thiên như hình dưới đây
Bài toán gốc Hàm số $y=f(x)$ đạt giá trị lớn nhất trên $[-4;0]$ tại điểm nào? Biết hàm số có bảng biến thiên như hình dưới đây A. $x_1=-1,x_2=-4$. B. $x_1=-1,x_2=0$. C. $x_1=-3,x_2=-4$. D. $x_1=-3,x_2=0$. Lời giải: $y=f(x)=-x^3-6x^2-9x+1$ Phân tích và Phương pháp giải Đây là dạng toán tìm giá trị lớn nhất (GTLN) của […]
Tìm giá trị nhỏ nhất của hàm số $y=\dfrac{-x+2}{-3x+3}$ trên $[4;2027]$.
Bài toán gốc Tìm giá trị nhỏ nhất của hàm số $y=\dfrac{-x+2}{-3x+3}$ trên $[4;2027]$. A. $-\dfrac{1}{9}$. B. $\dfrac{1}{3}$. C. $\dfrac{2}{9}$. D. $\dfrac{5}{9}$. Lời giải: Hạn chế máy tính Phân tích và Phương pháp giải Đây là dạng toán tìm giá trị lớn nhất và nhỏ nhất của hàm số nhất biến (dạng $y=\dfrac{ax+b}{cx+d}$) trên một […]
Hàm số $y= f(x) = 6x^4-3x^2-18$ đạt giá trị lớn nhất trên đoạn $[-1, 8]$ bằng
Bài toán gốc Hàm số $y= f(x) = 6x^4-3x^2-18$ đạt giá trị lớn nhất trên đoạn $[-1, 8]$ bằng A. $\max\limits_{x \in [-1, 8]} f(x) = 54$. B. $\max\limits_{x \in [-1, 8]} f(x) = 24366$. C. $\max\limits_{x \in [-1, 8]} f(x) = -\dfrac{147}{8}$. D. $\max\limits_{x \in [-1, 8]} f(x) = -138$. Lời giải: Trên đoạn […]
Cho hàm số $y=f(x)=-2x^4-2044x^2+2473$. Giá trị lớn nhất của hàm số trên $[-66;89]$ bằng
Bài toán gốc Cho hàm số $y=f(x)=-2x^4-2044x^2+2473$. Giá trị lớn nhất của hàm số trên $[-66;89]$ bằng A. $2473$. B. $2475$. C. $2472$. D. $2476$. Lời giải: Hạn chế máy tính Phân tích và Phương pháp giải Đây là bài toán tìm giá trị lớn nhất (GTLN) của hàm số bậc bốn trùng phương $y […]
Tìm giá trị lớn nhất của hàm số $y=f(x)$ trên $[-2;2]$ có đồ thị như hình dưới đây
Bài toán gốc Tìm giá trị lớn nhất của hàm số $y=f(x)$ trên $[-2;2]$ có đồ thị như hình dưới đây A. -2. B. 0. C. 2. D. -1. Lời giải: $y=f(x)=x^3-3x$ Phân tích và Phương pháp giải Bài toán yêu cầu tìm giá trị lớn nhất (GTLN) của hàm số trên một đoạn đóng. […]
Cho hàm số $y = f(x) = \dfrac{-2x^2-3x}{-2x+1}$. Khi đó giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên $[1, 6]$ lần lượt bằng
Bài toán gốc Cho hàm số $y = f(x) = \dfrac{-2x^2-3x}{-2x+1}$. Khi đó giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên $[1, 6]$ lần lượt bằng A. $\max\limits_{[1, 6]}f(x) = \dfrac{90}{11}$, $\min\limits_{[1, 6]}f(x) = \dfrac{9}{2}$. B. $\max\limits_{[1, 6]}f(x) = -1$, $\min\limits_{[1, 6]}f(x) = \dfrac{9}{2}$. C. $\max\limits_{[1, 6]}f(x) = -1$, $\min\limits_{[1, 6]}f(x) […]
Giá trị nhỏ nhất của hàm số $y=x+\dfrac{25}{x}$ trên $[2;8]$ bằng
Bài toán gốc Giá trị nhỏ nhất của hàm số $y=x+\dfrac{25}{x}$ trên $[2;8]$ bằng A. $\dfrac{89}{8}$. B. $10$. C. $-20$. D. $\dfrac{29}{2}$. Phân tích và Phương pháp giải Đây là bài toán tìm giá trị lớn nhất, nhỏ nhất của hàm số liên tục trên một đoạn kín (khoảng đóng). Phương pháp giải chuẩn là […]
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0\,;\,5} \right]\) và có bảng biến thiên như hình vẽ dưới đây Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {3x} + \sqrt {10 – 2x} = m\sqrt {f\left( x \right)} \) có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\)?
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0\,;\,5} \right]\) và có bảng biến thiên như hình vẽ dưới đây Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {3x} + \sqrt {10 – 2x} = m\sqrt {f\left( x \right)} \) có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\)? A […]
CASIO – TÍNH NHANH Max – Min Hàm số
CASIO – TÍNH NHANH Max – Min Hàm số ==== ===== ———– xem file pdf— ————– == LINK DOWNLOAD === DOWNLOAD PDF ————–