Bài toán gốc Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = x \sqrt{225 – x^2}$ A. $\max\limits_{\left[-15; 15\right]} f(x) = \dfrac{225}{2}$; $\min\limits_{\left[ -15; 15 \right]} f(x) = – \dfrac{225}{2}$. B. $\max\limits_{\left[-15; 15 \right]} f(x) = 0$; $\min\limits_{\left[ -15; 15 \right]} f(x) = – \dfrac{225}{2}$. C. $\max\limits_{\left[-15; 15 \right]} […]
Quiz - Max - Min
Mỗi trang giấy của một cuốn sách được qui định diện tích là 460 cm$^2$
Bài toán gốc Mỗi trang giấy của một cuốn sách được qui định diện tích là 460 cm$^2$. Khi trình bày nội dung lên trang giấy này người ta phải chừa trống lề trên và lề dưới là 3cm, lề trái và lề phải là 2cm. Biết diện tích của phần trình bày nội dung […]
Hàm số $y=f(x)=-x^3+3x+2+m$, gọi giá trị lớn nhất, nhỏ nhất của hàm số $y=f(x)$ trên $[-3;3]$ lần lượt là $a,b$. Tìm $m$ để $a+b=6$?
Bài toán gốc Hàm số $y=f(x)=-x^3+3x+2+m$, gọi giá trị lớn nhất, nhỏ nhất của hàm số $y=f(x)$ trên $[-3;3]$ lần lượt là $a,b$. Tìm $m$ để $a+b=6$? A. $1$. B. $2$. C. $0$. D. $-2$. Lời giải: $y(-1)=0+m,y(1)=4+m,y(-3)=20+m,y(3)=-16+m$ Phân tích và Phương pháp giải Đây là dạng toán tìm tham số m dựa trên điều […]
Tìm giá trị lớn nhất của hàm số $y=2+3\sqrt{-x^2+4x}$.
Bài toán gốc Tìm giá trị lớn nhất của hàm số $y=2+3\sqrt{-x^2+4x}$. A. $5$. B. $11$. C. $10$. D. $8$. Phân tích và Phương pháp giải Đây là dạng bài toán tìm Giá trị lớn nhất (GTLN) của hàm số chứa căn thức, có dạng $y = A + B\sqrt{u(x)}$ với $B>0$. Phương pháp giải […]
Hàm số $y=f(x)$ có bảng biến thiên của $f^{\prime}(x)$ như hình dưới đây: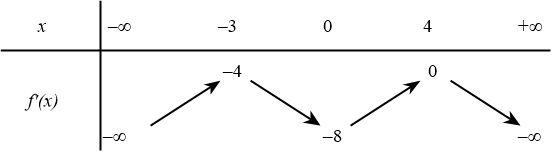
Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[3;4]$ bằng
Bài toán gốc Hàm số $y=f(x)$ có bảng biến thiên của $f^{\prime}(x)$ như hình dưới đây: Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[3;4]$ bằng A. $f(0)$. B. $f(4)$. C. $f(3)$. D. $f(-3)$. Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất, nhỏ nhất của hàm […]
Hàm số $y=f(x)=\dfrac{x-m^2}{x+4}$ với $m$ là tham số thực. Gọi $a,b$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên $[-8;-5]$. Tính tổng bình phương các giá trị $m$ để $a+b=27$?
Bài toán gốc Hàm số $y=f(x)=\dfrac{x-m^2}{x+4}$ với $m$ là tham số thực. Gọi $a,b$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên $[-8;-5]$. Tính tổng bình phương các giá trị $m$ để $a+b=27$? A. $32$. B. $35$. C. $29$. D. $31$. Phân tích và Phương pháp giải Đây […]
Cho hàm số $y=f(x)=-3x^4-2035x^2+2765$. Chọn phát biểu đúng?
Bài toán gốc Cho hàm số $y=f(x)=-3x^4-2035x^2+2765$. Chọn phát biểu đúng? A. Hàm số đạt giá trị lớn nhất trên $[-117;189]$ tại điểm $x=189$. B. Hàm số đạt giá trị lớn nhất trên $[-117;189]$ tại điểm $x=0$. C. Hàm số đạt giá trị nhỏ nhất trên $[-117;189]$ tại điểm $x=189$. D. Hàm số đạt giá […]
Tìm giá trị lớn nhất của hàm số $y=-x^3+3x+2$ trên $[-2;+\infty)$.
Bài toán gốc Tìm giá trị lớn nhất của hàm số $y=-x^3+3x+2$ trên $[-2;+\infty)$. A. $6$. B. $3$. C. $7$. D. $4$. Lời giải: Hạn chế máy tính Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất (GTLN) của hàm số bậc ba $y=f(x)$ trên một nửa khoảng […]
Tìm giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[-1;3]$ có đồ thị như hình dưới đây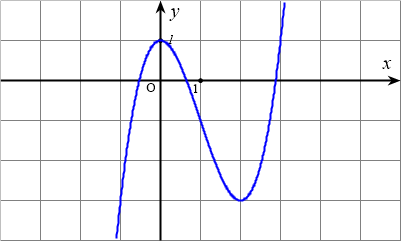
Bài toán gốc Tìm giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[-1;3]$ có đồ thị như hình dưới đây A. 1. B. -3. C. -2. D. 0. Lời giải: $y=f(x)=x^3-3x^2+1$ Phân tích và Phương pháp giải Đây là dạng toán tìm giá trị lớn nhất hoặc giá trị nhỏ nhất (GTLN, GTNN) của […]
Tìm giá trị lớn nhất của hàm số $f(x)=x^3+3x^2+1$ trên $[-3;2]$.
Bài toán gốc Tìm giá trị lớn nhất của hàm số $f(x)=x^3+3x^2+1$ trên $[-3;2]$. A. 5. B. 21. C. 23. D. 1. Phân tích và Phương pháp giải Đây là dạng toán tìm giá trị lớn nhất (GTLN) của hàm số liên tục trên một đoạn đóng. Phương pháp giải là: Tính đạo hàm $f'(x)$, […]