Bài toán gốc Một nông dân có 40 m hàng rào và muốn rào lại mảnh đất hình chữ nhật tiếp giáp với một con sông. Ông không cần rào cho phía giáp bờ sông. Hỏi ông có thể rào được mảnh đất có diện tích lớn nhất là bao nhiêu? A. $199$. B. $200$. […]
Quiz - Max - Min
Hàm số $y=f(x)=\dfrac{x-m^2}{x+3}$ với $m$ là tham số thực. Tính tổng bình phương các giá trị $m$ để giá trị lớn nhất của hàm số trên $[-6;-4]$ bằng $8$?
Bài toán gốc Hàm số $y=f(x)=\dfrac{x-m^2}{x+3}$ với $m$ là tham số thực. Tính tổng bình phương các giá trị $m$ để giá trị lớn nhất của hàm số trên $[-6;-4]$ bằng $8$? A. $10$. B. $7$. C. $8$. D. $6$. Phân tích và Phương pháp giải Đây là dạng bài toán tìm tham số m […]
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C. Khoảng cách ngắn nhất từ C đến B là 3 km. Khoảng cách từ B đến A là 12 km
Bài toán gốc Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C. Khoảng cách ngắn nhất từ C đến B là 3 km. Khoảng cách từ B đến A là 12 km. Mỗi km dây điện đặt dưới nước mất 5000 USD, còn đặt dưới […]
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp có đáy hình vuông cạnh $x$ , đường cao $h$ và diện tích bề mặt bằng $S = 190 \text{cm}^2$
Bài toán gốc Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp có đáy hình vuông cạnh $x$ , đường cao $h$ và diện tích bề mặt bằng $S = 190 \text{cm}^2$. Khi đó thể tích của hộp là lớn nhất bằng bao nhiêu? A. […]
Một cửa hàng bán bưởi với giá bán là 50.000 đồng/kg. Với giá bán này thì cửa hàng chỉ bán được khoảng 40 kg bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi kg 5000 đồng thì số bưởi bán được tăng thêm 20 kg
Bài toán gốc Một cửa hàng bán bưởi với giá bán là 50.000 đồng/kg. Với giá bán này thì cửa hàng chỉ bán được khoảng 40 kg bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi kg 5000 đồng thì số bưởi bán được tăng thêm 20 […]
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C. Khoảng cách ngắn nhất từ C đến B là 2 km. Khoảng cách từ B đến A là 9 km.
Bài toán gốc Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C. Khoảng cách ngắn nhất từ C đến B là 2 km. Khoảng cách từ B đến A là 9 km. Mỗi km dây điện đặt dưới nước mất 5000 USD, còn đặt dưới […]
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = \sqrt{x – 6} + \sqrt{10 – x}$ trên đoạn $[6, 10]$.
Bài toán gốc Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x) = \sqrt{x – 6} + \sqrt{10 – x}$ trên đoạn $[6, 10]$. A. $\max\limits_{\left[ 6;10\right]} f(x) = 2$; $\min\limits_{\left[ 6;10\right]} f(x) = 2 \sqrt{2}$. B. $\max\limits_{\left[ 6;10\right]} f(x) = 2 \sqrt{2}$; $\min\limits_{\left[ 6;10\right]} f(x) = 0$. C. $\max\limits_{\left[ […]
Tìm giá trị lớn nhất của hàm số $f(x) = 3 + 3x – e^x$ trên đoạn $[0; 5]$
Bài toán gốc Tìm giá trị lớn nhất của hàm số $f(x) = 3 + 3x – e^x$ trên đoạn $[0; 5]$ A. $\max\limits_{\left[0; 5\right]} f(x) = 18 – e^{5}$. B. $\max\limits_{\left[0; 5\right]} f(x) = \ln{\left(27 \right)}$. C. $\max\limits_{\left[0; 5\right]} f(x) = 15$. D. $\max\limits_{\left[0; 5\right]} f(x) = 3\sqrt{5}$. Lời giải: Trên đoạn $[0; 5]$ […]
Hàm số $y=f(x)$ có bảng biến thiên của $f^{\prime}(x)$ như hình dưới đây:
Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[2;7]$ bằng
Bài toán gốc Hàm số $y=f(x)$ có bảng biến thiên của $f^{\prime}(x)$ như hình dưới đây: Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[2;7]$ bằng A. $f(2)$. B. $f(7)$. C. $f(0)$. D. $f(4)$. Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất/nhỏ nhất của hàm số […]
Hàm số $y=f(x)$ có $y=f^{\prime}(x)=ax^2+bx+c$ có đồ thị như hình dưới đây: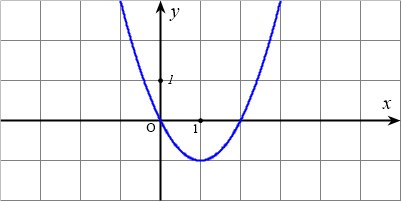
Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[1;3]$ bằng
Bài toán gốc Hàm số $y=f(x)$ có $y=f^{\prime}(x)=ax^2+bx+c$ có đồ thị như hình dưới đây: Giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[1;3]$ bằng A. $f(1)$. B. $f(0)$. C. $f(3)$. D. $f(2)$. Lời giải: $y^{\prime}=x^2-2x$ Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất, nhỏ nhất […]