Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp có đáy hình vuông cạnh $x$ , đường cao $h$ và diện tích bề mặt bằng $S = 190 \text{cm}^2$

Bài toán gốc

Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp có đáy hình vuông cạnh $x$ , đường cao $h$ và diện tích bề mặt bằng $S = 190 \text{cm}^2$. Khi đó thể tích của hộp là lớn nhất bằng bao nhiêu?

A. $\dfrac{\sqrt{570}}{3}$.

B. $\sqrt{3}$.

C. $\dfrac{95 \sqrt{570}}{9}$.

D. $5\sqrt{3}$.

Lời giải: Ta có diện tích bề mặt của hộp là $S = x^2 + 4xh$, với $x$ là cạnh đáy và $h$ là chiều cao.
Với $S = 190$, ta có $h = \dfrac{S – x^2}{4x}$.
Thể tích của hộp là $V = x^2h = x^2 \left(\dfrac{S – x^2}{4x}\right) = \dfrac{x(190 – x^2)}{4}$.
Ta có $V'(x) = \dfrac{95}{2} – \dfrac{3 x^{2}}{4}$; $V'(x) = 0$, ta được $x = \dfrac{\sqrt{570}}{3}, (x {>} 0)$.
Lập bảng biến thiên

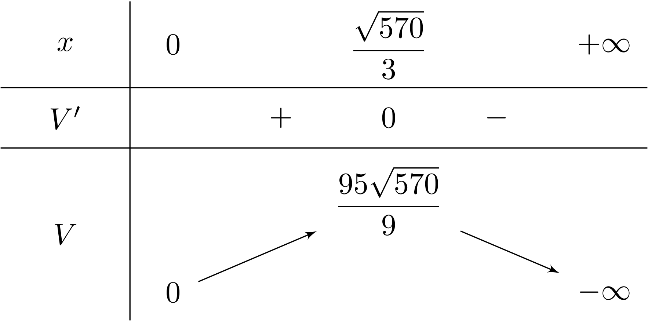
Thể tích lớn nhất của hộp là $V = \dfrac{95 \sqrt{570}}{9}$ tại $x = \dfrac{\sqrt{570}}{3}$.

Phân tích và Phương pháp giải

Đây là dạng toán tối ưu hóa (tìm giá trị lớn nhất) trong ứng dụng đạo hàm. Phương pháp giải là sử dụng điều kiện ràng buộc (diện tích bề mặt cố định) để biểu diễn thể tích $V$ dưới dạng hàm một biến $x$. Sau đó, sử dụng đạo hàm $V'(x)$ để tìm điểm cực trị, từ đó xác định giá trị lớn nhất của thể tích.

Bài toán tương tự

Một người thợ cần làm một chiếc thùng đựng nước hình hộp chữ nhật không nắp, có đáy là hình vuông. Biết rằng tổng diện tích vật liệu làm thùng (diện tích bề mặt) là $S = 48 ext{ m}^2$. Hỏi thể tích lớn nhất mà chiếc thùng này có thể chứa được là bao nhiêu?

A. $16 ext{ m}^3$
B. $24 ext{ m}^3$
C. $32 ext{ m}^3$
D. $36 ext{ m}^3$

Đáp án đúng: C. $32 ext{ m}^3$

Lời giải ngắn gọn:
Gọi $x$ là cạnh đáy, $h$ là chiều cao. Diện tích bề mặt $S = x^2 + 4xh = 48$. Thể tích $V = x^2h$.
Từ $S$, ta có $h = \frac{48 – x^2}{4x}$.
Thể tích $V(x) = x^2 \left(\frac{48 – x^2}{4x}\right) = 12x – \frac{x^3}{4}$.
Đạo hàm $V'(x) = 12 – \frac{3x^2}{4}$. Cho $V'(x) = 0 \implies x^2 = 16 \implies x = 4$ (vì $x>0$).
$V_{max} = V(4) = 12(4) – \frac{4^3}{4} = 48 – 16 = 32 ext{ m}^3$.