Quiz - Max - Min

Bài toán gốc Hàm số $y= f(x) = -3x^3+3x^2+3x+6$ đạt giá trị lớn nhất trên đoạn $[2, 3]$ bằng?A. $\max\limits_{x \in [2, 3]} f(x) = -39$.B. $\max\limits_{x \in [2, 3]} f(x) = 6$.C. $\max\limits_{x \in [2, 3]} f(x) = 6$.D. $\max\limits_{x \in [2, 3]} f(x) = 0$.Lời giải: Trên đoạn $[2, 3]$, ta có Đạo hàm $f^{\prime}(x) = -9x^2+6x+3$. Cho $f^{\prime}(x)= 0 \Leftrightarrow … [Đọc thêm...] vềHàm số $y= f(x) = -3x^3+3x^2+3x+6$ đạt giá trị lớn nhất trên đoạn $[2, 3]$ bằng?

Bài toán gốc Tìm giá trị nhỏ nhất của hàm số $y=-x^3-3x^2-2$ trên $[-4;102]$.A. $-1092425$.B. $-1092422$.C. $-1092421$.D. $-1092419$.Lời giải: Hạn chế máy tính Phân tích và Phương pháp giải Đây là bài toán tìm giá trị lớn nhất/nhỏ nhất (GTLN/GTNN) của hàm số đa thức trên một đoạn kín (tức là trên đoạn $[a; b]$). Phương pháp giải chuẩn là sử dụng … [Đọc thêm...] vềTìm giá trị nhỏ nhất của hàm số $y=-x^3-3x^2-2$ trên $[-4;102]$.

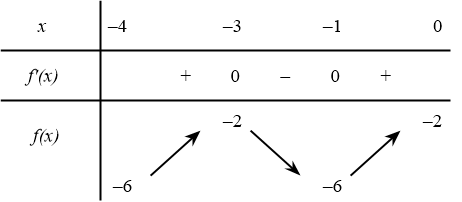
Bài toán gốc Tìm giá trị lớn nhất của hàm số $y=f(x)$ trên $[-4;0]$ có bảng biến thiên như hình dưới đâyA. -6.B. -2.C. -3.D. 1.Lời giải: $y=f(x)=x^3+6x^2+9x-2$ Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất (GTLN) của hàm số đa thức trên một đoạn đóng (cụ thể là hàm bậc ba). Phương pháp giải chuẩn mực là sử dụng đạo … [Đọc thêm...] vềTìm giá trị lớn nhất của hàm số $y=f(x)$ trên $[-4;0]$ có bảng biến thiên như hình dưới đây

Bài toán gốc Hàm số $f(x)=x^3+3x^2-1$ đạt giá trị lớn nhất trên $[-4;2]$ tại điểm có hoành độ bằng bao nhiêu?A. -4.B. -2.C. 19.D. 2. Phân tích và Phương pháp giải Đây là dạng toán tìm giá trị lớn nhất (GTLN) của hàm số liên tục trên một đoạn đóng $[a; b]$. Phương pháp giải chung là: (1) Tính đạo hàm $f'(x)$. (2) Tìm các nghiệm $x_i$ của phương … [Đọc thêm...] vềHàm số $f(x)=x^3+3x^2-1$ đạt giá trị lớn nhất trên $[-4;2]$ tại điểm có hoành độ bằng bao nhiêu?

Bài toán gốc Cho hàm số $f(x) = \dfrac{x+3}{x+3}$. Giá trị lớn nhất của hàm số trên đoạn $[-2, 8]$ làA. $8$.B. $3$.C. $\dfrac{3}{11}$.D. $3$.Lời giải: Trên đoạn $[-2, 8]$, ta có $f(-2)=3$ và $f(8)=\dfrac{3}{11}$. Do đó giá trị lớn nhất bằng $3$ Phân tích và Phương pháp giải Đây là dạng toán tìm Giá trị lớn nhất (GTLN) của hàm số liên tục trên … [Đọc thêm...] vềCho hàm số $f(x) = \dfrac{x+3}{x+3}$. Giá trị lớn nhất của hàm số trên đoạn $[-2, 8]$ là

Bài toán gốc Hàm số $f(x)=x^3-3x+2$ đạt giá trị nhỏ nhất trên $[-3;2]$ tại điểm có hoành độ bằng bao nhiêu?A. -3.B. 2.C. -16.D. 1. Phân tích và Phương pháp giải Đây là dạng toán tìm giá trị nhỏ nhất (hoặc lớn nhất) của hàm số liên tục trên một đoạn kín (Tên gọi chính thức: Bài toán GTLN, GTNN trên đoạn). Phương pháp giải bao gồm các bước: 1. … [Đọc thêm...] vềHàm số $f(x)=x^3-3x+2$ đạt giá trị nhỏ nhất trên $[-3;2]$ tại điểm có hoành độ bằng bao nhiêu?

Bài toán gốc Tìm giá trị nhỏ nhất của hàm số $y=-x^3+3x+2$ trên $[-2;2]$.A. 0.B. 3.C. 1.D. 4. Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất và nhỏ nhất (GTLN/GTNN) của hàm số đa thức trên một đoạn đóng (tức là tập xác định là một đoạn [a; b]). Phương pháp giải chuẩn là sử dụng đạo hàm:1. Tính đạo hàm y' và tìm các điểm … [Đọc thêm...] vềTìm giá trị nhỏ nhất của hàm số $y=-x^3+3x+2$ trên $[-2;2]$

Bài toán gốc Tìm giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[-3;2]$ có bảng biến thiên như hình dưới đâyA. 2.B. 0.C. 4.D. 20.Lời giải: $y=f(x)=-x^3+3x+2$ Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số trên một đoạn đóng $[a; b]$. Phương pháp giải chung là sử dụng đạo hàm để … [Đọc thêm...] vềTìm giá trị nhỏ nhất của hàm số $y=f(x)$ trên $[-3;2]$ có bảng biến thiên như hình dưới đây

Bài toán gốc Hàm số $y=x+\dfrac{9}{x}$ đạt giá trị lớn nhất trên $[2;5]$ tại điểmA. $x=2$.B. $x=3$.C. $x=5$.D. $x=6$. Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất (GTLN) của hàm số trên một đoạn đóng. Phương pháp giải chuẩn là sử dụng đạo hàm:1. Tính đạo hàm $y'$.2. Tìm các điểm cực trị $x_0$ trong đoạn $[a; b]$ bằng … [Đọc thêm...] vềHàm số $y=x+\dfrac{9}{x}$ đạt giá trị lớn nhất trên $[2;5]$ tại điểm

Bài toán gốc Hàm số $y=x+\dfrac{16}{x}$ đạt giá trị nhỏ nhất trên $[3;6]$ tại điểmA. $x=3$.B. $x=4$.C. $x=8$.D. $x=6$. Phân tích và Phương pháp giải Đây là dạng bài toán tìm giá trị lớn nhất (GTLN) hoặc giá trị nhỏ nhất (GTNN) của hàm số trên một đoạn đóng. Phương pháp giải chung là sử dụng đạo hàm để khảo sát sự biến thiên của hàm số trên đoạn … [Đọc thêm...] vềHàm số $y=x+\dfrac{16}{x}$ đạt giá trị nhỏ nhất trên $[3;6]$ tại điểm