Khảo sát và vẽ đồ thị hàm số

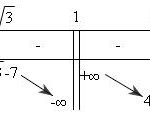
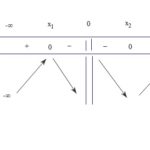
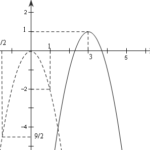
Đề bài: Cho hàm số $y = f(x) = {x^4} + 2m{x^2} + m$, m là tham số$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =-1.$$2$. Tìm tất cả các giá trị của $m$ để hàm số $f(x) > 0$ với mọi $x$.Với các giá trị $m$ tìm được ở trên, chứng minh rằng hàm số :$F(x) = f(x) + f'(x) + f''(x) + f'''(x) + {f^{(4)}}x > 0  \forall x$$(f^{(4)} (x$) là kí hiệu … [Đọc thêm...] vềĐề: Cho hàm số $y = f(x) = {x^4} + 2m{x^2} + m$, m là tham số$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =-1.$$2$. Tìm tất cả các giá trị của $m$ để hàm số $f(x) > 0$ với mọi $x$.Với các giá trị $m$ tìm được ở trên, chứng minh rằng hàm số :$F(x) = f(x) + f'(x) + f''(x) + f'''(x) + {f^{(4)}}x > 0  \forall x$$(f^{(4)} (x$) là kí hiệu đạo hàm cấp $4$ của hàm số $f(x)$ tại điểm $x)$

Đề bài: Cho hàm số        $y = {(x + 1)^2}(2 - x)$1) Khảo sát sự biến thiên và vẽ đồ thị hàm số.2) Dựa vào đồ thị, biện luận theo $m$ số nghiệm của phương trình ${(x + 1)^2}(2 - x) = {(m + 1)^2}(2 - m)$ Lời giải $1)$ Hàm số xác định với mọi x.Ta có$y' = 2(x + 1)(2 - x) - {(x + 1)^2} = 3(x + 1)(1 - x)$;$y'' = 3(1 - x) - 3(1 + x) =  - 6x$Bạn đọc vẽ bảng biến thiên và đồ thị … [Đọc thêm...] vềĐề: Cho hàm số        $y = {(x + 1)^2}(2 – x)$1) Khảo sát sự biến thiên và vẽ đồ thị hàm số.2) Dựa vào đồ thị, biện luận theo $m$ số nghiệm của phương trình ${(x + 1)^2}(2 – x) = {(m + 1)^2}(2 – m)$

Đề bài: Cho hàm:  $f(x) =  - {x^4} + 2(m + 1){x^2} - 2m - 1$.a) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m = 0$.b) Xác định tham số $m$ để $f(x) = 0$ có bốn nghiệm phân biệt tạo thành cấp số cộng Lời giải a) Dành cho bạn đọc.b) Ta có:  $f(x) = 0 \Leftrightarrow {x^4} - 2(m + 1){x^2} - 2m - 1 = 0$$ \Leftrightarrow {\left[ {{x^2} - (m + 1)} \right]^2} - {m^2} = 0$    … [Đọc thêm...] vềĐề: Cho hàm:  $f(x) =  – {x^4} + 2(m + 1){x^2} – 2m – 1$.a) Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m = 0$.b) Xác định tham số $m$ để $f(x) = 0$ có bốn nghiệm phân biệt tạo thành cấp số cộng

Đề bài: Cho hàm số$y=\frac{ 1}{4}x^{3} -\frac{ 3}{2}x^{2}+5$a)    Khảo sát và vẽ đồ thị của hàm số.b)    Tìm các giá trị của m để phương trình $x^{3}-6 x^{2} +m=0$ có ba nghiệm  thực phân biệt. Lời giải  $y= \frac{ 1}{4}x^{3}- \frac{ 3}{2} x^{2} +5$a)    •    Tập xác định: D= R•    Sự biến thiên: $y’= \frac{ 4}{3} x^{2} -3x =0 \Leftrightarrow \left[ \begin{array}{l}   x=0 … [Đọc thêm...] vềĐề: Cho hàm số$y=\frac{ 1}{4}x^{3} -\frac{ 3}{2}x^{2}+5$a)    Khảo sát và vẽ đồ thị của hàm số.b)    Tìm các giá trị của m để phương trình $x^{3}-6 x^{2} +m=0$ có ba nghiệm  thực phân biệt.

Đề bài: Khảo sát và vẽ đồ thị hàm số $y=F(x)=\begin{cases}-x+\frac{3}{2}    nếu  x\leq -\frac{1}{2} \\ -2x^2+x+3,  nếu  x>-\frac{1}{2} \end{cases}$ Lời giải Giải* Xét hàm số bậc nhất $f_1(X)=-x+\frac{3}{2}$ trên khoảng $D_1=(-\infty; -\frac{1}{2}]$Đó là hàm số bậc nhất có $a=-1Tại $x=-\frac{1}{2}, f(-\frac{1}{2})=2$. Tại $x=\frac{3}{2}, f(\frac{3}{2})=0$Đồ thị là đường … [Đọc thêm...] vềĐề: Khảo sát và vẽ đồ thị hàm số $y=F(x)=\begin{cases}-x+\frac{3}{2}    nếu  x\leq -\frac{1}{2} \\ -2x^2+x+3,  nếu  x>-\frac{1}{2} \end{cases}$

Đề bài: Cho hàm số : $y= - x^{4}- x^{2}+6$a)    Khảo sát sự biến thiên và vẽ đồ thị  (C) của hàm số đã cho.b)    Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng $y= \frac{ 1}{6}x-1$ Lời giải a)    •    Tập xác định : $D=R$•    Sự biến thiên : $y’=-4x^{3}-2x=-2x \left( 2 x^{2} +1   \right) =0$$\Leftrightarrow x=0 \Rightarrow y=6$Bảng … [Đọc thêm...] vềĐề: Cho hàm số : $y= – x^{4}- x^{2}+6$a)    Khảo sát sự biến thiên và vẽ đồ thị  (C) của hàm số đã cho.b)    Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng $y= \frac{ 1}{6}x-1$

Đề bài: $1$. Khảo sát hàm số \(y = \frac{{{x^2} + x - 5}}{{x - 2}}\left( C \right)\)$2$. Chứng minh rằng tích các khoảng cách từ một điểm $M$ bất kỳ trên đồ thị $(C)$ đến các tiệm cận là một hằng số không phụ thuộc vị trí điểm $M$$3$. Tìm trên mỗi nhánh của $(C)$ một điểm sao cho khoảng cách giữa chúng nhỏ nhất Lời giải $1$. Bạn đọc tự giải.$2$. Đồ thị có tiệm cận đứng \(x … [Đọc thêm...] vềĐề: $1$. Khảo sát hàm số \(y = \frac{{{x^2} + x – 5}}{{x – 2}}\left( C \right)\)$2$. Chứng minh rằng tích các khoảng cách từ một điểm $M$ bất kỳ trên đồ thị $(C)$ đến các tiệm cận là một hằng số không phụ thuộc vị trí điểm $M$$3$. Tìm trên mỗi nhánh của $(C)$ một điểm sao cho khoảng cách giữa chúng nhỏ nhất