Đề bài: Cho hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\)$1$. Khảo sát và vẽ đồ thị hàm số$2$. Tìm trên đồ thị hàm số đã cho các điểm sao cho tiếp tuyến tại đó của đồ thị vuông góc với tiệm cận xiên của nó. Lời giải $1$. Bạn đọc tự giải$2$. Tiệm cận xiên của đồ thị có PT : $y=x+1$.Gọi $x_0$ là hoành độ điểm cần tìm thì $x_0$ là nghiệm của phương trình \(f'\left( x_0 … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} + 2x + 2}}{{x + 1}}\)$1$. Khảo sát và vẽ đồ thị hàm số$2$. Tìm trên đồ thị hàm số đã cho các điểm sao cho tiếp tuyến tại đó của đồ thị vuông góc với tiệm cận xiên của nó.
Khảo sát và vẽ đồ thị hàm số
Đề: Cho hàm số: $y = \frac{{{x^2} – x + 1}}{{x – 1}}$1) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2) Tìm trên trục $Oy$ các điểm từ đó có thể kẻ được ít nhất một tiếp tuyến đến đồ thị $(C)$.3) Xác định $a$ để đồ thị $(C)$ tiếp xúc với parabol $y = {x^2} + a$
Đề bài: Cho hàm số: $y = \frac{{{x^2} - x + 1}}{{x - 1}}$1) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2) Tìm trên trục $Oy$ các điểm từ đó có thể kẻ được ít nhất một tiếp tuyến đến đồ thị $(C)$.3) Xác định $a$ để đồ thị $(C)$ tiếp xúc với parabol $y = {x^2} + a$ Lời giải $1)$ Dành cho bạn đọc.$2)$ Tìm $A(0, b)$ là một điểm trên trục $Oy$ mà tiếp … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{{{x^2} – x + 1}}{{x – 1}}$1) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2) Tìm trên trục $Oy$ các điểm từ đó có thể kẻ được ít nhất một tiếp tuyến đến đồ thị $(C)$.3) Xác định $a$ để đồ thị $(C)$ tiếp xúc với parabol $y = {x^2} + a$
Đề: Cho hàm số :$y = \frac{{(m + 1){x^2} – {m^2}}}{{x – m}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 1.$$2.$ Trong trường hợp tổng quát, chứng minh rằng với mọi giá trị $m \ne 0$, tiệm cận xiên của đồ thị hàm số luôn tiếp xúc với một Parabol cố định. Hãy chỉ rõ phương trình của Paralbol ấy.
Đề bài: Cho hàm số :$y = \frac{{(m + 1){x^2} - {m^2}}}{{x - m}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 1.$$2.$ Trong trường hợp tổng quát, chứng minh rằng với mọi giá trị $m \ne 0$, tiệm cận xiên của đồ thị hàm số luôn tiếp xúc với một Parabol cố định. Hãy chỉ rõ phương trình của Paralbol ấy. Lời giải $1$. Dành cho bạn đọc tự giải.$2$. $y = \frac{{(m … [Đọc thêm...] vềĐề: Cho hàm số :$y = \frac{{(m + 1){x^2} – {m^2}}}{{x – m}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 1.$$2.$ Trong trường hợp tổng quát, chứng minh rằng với mọi giá trị $m \ne 0$, tiệm cận xiên của đồ thị hàm số luôn tiếp xúc với một Parabol cố định. Hãy chỉ rõ phương trình của Paralbol ấy.
Đề: Cho hàm số: $y = {x^3} + 3{x^2} + 3x + 5$.1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng trên đồ thị không tồn tại 2 điểm sao cho hai tiếp tuyến tại 2 điểm đó của đồ thị là vuông góc với nhau.3) Xác định k để trên đồ thị có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng $y = kx$
Đề bài: Cho hàm số: $y = {x^3} + 3{x^2} + 3x + 5$.1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng trên đồ thị không tồn tại 2 điểm sao cho hai tiếp tuyến tại 2 điểm đó của đồ thị là vuông góc với nhau.3) Xác định k để trên đồ thị có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng $y = kx$ Lời giải $1)$ Dành cho bạn đọc.$2)$ Giả sử có 2 … [Đọc thêm...] vềĐề: Cho hàm số: $y = {x^3} + 3{x^2} + 3x + 5$.1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng trên đồ thị không tồn tại 2 điểm sao cho hai tiếp tuyến tại 2 điểm đó của đồ thị là vuông góc với nhau.3) Xác định k để trên đồ thị có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng $y = kx$
Đề: Cho hàm số: $y = {x^3} – mx + m – 2$, $m$ là tham số1) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số khi $m = 3$.2) Dùng đồ thị $(C)$, biện luận theo $k$ số nghiệm của phương trình ${x^3} – 3x – k + 1 = 0$.3) Gọi $(Cm)$ là đồ thị của hàm số đã cho. Chứng minh rằng tiếp tuyến của $(Cm)$ tại điểm uốn của nó đi qua một điểm cố định khi $m$ thay đổi
Đề bài: Cho hàm số: $y = {x^3} - mx + m - 2$, $m$ là tham số1) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số khi $m = 3$.2) Dùng đồ thị $(C)$, biện luận theo $k$ số nghiệm của phương trình ${x^3} - 3x - k + 1 = 0$.3) Gọi $(Cm)$ là đồ thị của hàm số đã cho. Chứng minh rằng tiếp tuyến của $(Cm)$ tại điểm uốn của nó đi qua một điểm cố định khi $m$ thay đổi Lời giải … [Đọc thêm...] vềĐề: Cho hàm số: $y = {x^3} – mx + m – 2$, $m$ là tham số1) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số khi $m = 3$.2) Dùng đồ thị $(C)$, biện luận theo $k$ số nghiệm của phương trình ${x^3} – 3x – k + 1 = 0$.3) Gọi $(Cm)$ là đồ thị của hàm số đã cho. Chứng minh rằng tiếp tuyến của $(Cm)$ tại điểm uốn của nó đi qua một điểm cố định khi $m$ thay đổi
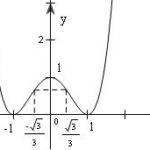
Đề: $1$. Giải phương trình: $x^4 – 2x^2 + 1 = 0$$2$. Khảo sát hàm số: $y = x^4 – 2x^2 + 1$$3$. Biện luận theo $m$ số nghiệm của phương trình: $x^4 – 2x^2 + 1- m = 0$
Đề bài: $1$. Giải phương trình: $x^4 - 2x^2 + 1 = 0$$2$. Khảo sát hàm số: $y = x^4 - 2x^2 + 1$$3$. Biện luận theo $m$ số nghiệm của phương trình: $x^4 - 2x^2 + 1- m = 0$ Lời giải $1.$ Ta có $x^4-2x^2+1=(x^2-1)^2=0\Leftrightarrow x=\pm1$$2.$ Khảo sát hàm số: xin dành cho bạn đọc, đồ thị hàm số như hình vẽ:$3.$ Nghiệm phương trình là hoành độ giao diểm của hai … [Đọc thêm...] vềĐề: $1$. Giải phương trình: $x^4 – 2x^2 + 1 = 0$$2$. Khảo sát hàm số: $y = x^4 – 2x^2 + 1$$3$. Biện luận theo $m$ số nghiệm của phương trình: $x^4 – 2x^2 + 1- m = 0$
Đề: Cho hàm: $y = \frac{{{x^2} + x – 3}}{{x + 2}}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ kết quả đó, hãy suy ra cách vẽ đồ thị của hàm số: $y = \frac{{{x^2} + x – 3}}{{\left| {x + 2} \right|}}$3) Tìm các điểm thuộc trục hoành sao cho từ mỗi điểm ấy có thể vẽ được đúng một tiếp tuyến tới đồ thị ở phần 1
Đề bài: Cho hàm: $y = \frac{{{x^2} + x - 3}}{{x + 2}}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ kết quả đó, hãy suy ra cách vẽ đồ thị của hàm số: $y = \frac{{{x^2} + x - 3}}{{\left| {x + 2} \right|}}$3) Tìm các điểm thuộc trục hoành sao cho từ mỗi điểm ấy có thể vẽ được đúng một tiếp tuyến tới đồ thị ở phần 1 Lời giải $1)$ Viết … [Đọc thêm...] vềĐề: Cho hàm: $y = \frac{{{x^2} + x – 3}}{{x + 2}}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ kết quả đó, hãy suy ra cách vẽ đồ thị của hàm số: $y = \frac{{{x^2} + x – 3}}{{\left| {x + 2} \right|}}$3) Tìm các điểm thuộc trục hoành sao cho từ mỗi điểm ấy có thể vẽ được đúng một tiếp tuyến tới đồ thị ở phần 1
Đề: Cho hàm số:$y = \frac{{{x^2} – x – 1}}{{x – 3}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Tìm $m$ để phương trình:${x^2} – (m + 1)x + 3m – 5 = 0$ có $2$ nghiệm dương.
Đề bài: Cho hàm số:$y = \frac{{{x^2} - x - 1}}{{x - 3}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Tìm $m$ để phương trình:${x^2} - (m + 1)x + 3m - 5 = 0$ có $2$ nghiệm dương. Lời giải $1.$ Xin dành cho bạn đọc. $\begin{array}{l}2.\,\,\,{x^2} - (m + 1)x + 3m - 5 = 0\\ \Leftrightarrow \frac{{{x^2} - x - 5}}{{x - 3}} = m\end{array}$Nghiệm phương trình là hoành độ … [Đọc thêm...] vềĐề: Cho hàm số:$y = \frac{{{x^2} – x – 1}}{{x – 3}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Tìm $m$ để phương trình:${x^2} – (m + 1)x + 3m – 5 = 0$ có $2$ nghiệm dương.
Đề: $1$. Khảo sát và vẽ đồ thị hàm số: $y = \frac{x^2+ 4x + 5}{x + 2}$Tìm các điểm trên đồ thị có khoảng cách đến đường thẳng $y + 3x + 6 = 0$ là nhỏ nhất.$2$. Tính diện tích hình phẳng được giới hạn bởi các đường: $y = \frac{1}{\sin 2x}\,;\,\, y = \frac{1}{cos2x};x = \frac{\pi }{6};x = \frac{\pi }{3}$
Đề bài: $1$. Khảo sát và vẽ đồ thị hàm số: $y = \frac{x^2+ 4x + 5}{x + 2}$Tìm các điểm trên đồ thị có khoảng cách đến đường thẳng $y + 3x + 6 = 0$ là nhỏ nhất.$2$. Tính diện tích hình phẳng được giới hạn bởi các đường: $y = \frac{1}{\sin 2x}\,;\,\, y = \frac{1}{cos2x};x = \frac{\pi }{6};x = \frac{\pi }{3}$ Lời giải $1.$ $y = \frac{x^2+ 4x + 5}{x + … [Đọc thêm...] vềĐề: $1$. Khảo sát và vẽ đồ thị hàm số: $y = \frac{x^2+ 4x + 5}{x + 2}$Tìm các điểm trên đồ thị có khoảng cách đến đường thẳng $y + 3x + 6 = 0$ là nhỏ nhất.$2$. Tính diện tích hình phẳng được giới hạn bởi các đường: $y = \frac{1}{\sin 2x}\,;\,\, y = \frac{1}{cos2x};x = \frac{\pi }{6};x = \frac{\pi }{3}$
Đề: Xét hàm số với tham số $a:$ \(y = 2{x^3} + ax^2 – 12x – 13\) 1. Với những giá trị nào của $a$ thì đồ thị của hàm số có điểm cực đại và điểm cực tiểu và các điểm này cách đều trực tung?2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số ứng với $a = 3.$
Đề bài: Xét hàm số với tham số $a:$ \(y = 2{x^3} + ax^2 - 12x - 13\) 1. Với những giá trị nào của $a$ thì đồ thị của hàm số có điểm cực đại và điểm cực tiểu và các điểm này cách đều trực tung?2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số ứng với $a = 3.$ Lời giải $1$.Ta có \(y' = 6{x^2} + 2ax - 12\) luôn có hai nghiệm phân biệt \({x_{1,2}} = \frac{{ - a \pm \sqrt … [Đọc thêm...] vềĐề: Xét hàm số với tham số $a:$ \(y = 2{x^3} + ax^2 – 12x – 13\) 1. Với những giá trị nào của $a$ thì đồ thị của hàm số có điểm cực đại và điểm cực tiểu và các điểm này cách đều trực tung?2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số ứng với $a = 3.$