Đề bài: Cho elip $(E): \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $ với $F_1(-c;0)$. Tìm $M$ sao cho $MF_1$ ngắn nhất. Lời giải Ta có: $MF_1=a+ex_M$ Mà $M \in (E) \Rightarrow -a \leq x_M \Rightarrow -ea \leq ex_M \Rightarrow a-ea \leq a+ex_M=MF_1$Do đó $MF_1$ ngắn nhất $\Leftrightarrow MF_1=a-\frac{c}{a}a=a-c \Leftrightarrow … [Đọc thêm...] vềĐề: Cho elip $(E): \frac{x^2}{a^2}+\frac{y^2}{b^2}=1 $ với $F_1(-c;0)$. Tìm $M$ sao cho $MF_1$ ngắn nhất.
Giá trị lớn nhất - nhỏ nhất
Đề: Cho $x>0,y>0$ và $xy=4$. Tìm giá trị nhỏ nhất của:a) $P(x;y)=x^2+y^2$. b) $Q(x;y)=(x+1)(4y+3)$
Đề bài: Cho $x>0,y>0$ và $xy=4$. Tìm giá trị nhỏ nhất của:a) $P(x;y)=x^2+y^2$. b) $Q(x;y)=(x+1)(4y+3)$ Lời giải a) $P(x;y)=x^2+y^2=(x+y)^2-2xy=(x+y)^2-8$Theo hệ quả của bất đẳng thức Côsi cho x và y dương:$(x+y)^2\geq 4xy=16$. Tích $xy=4$ là hằng số nên tổng $x+y$ nhỏ nhất khi $x=y=2$.Vậy: min $P(x;y)=4^2-8=8$ đạt được khi … [Đọc thêm...] vềĐề: Cho $x>0,y>0$ và $xy=4$. Tìm giá trị nhỏ nhất của:a) $P(x;y)=x^2+y^2$. b) $Q(x;y)=(x+1)(4y+3)$
Đề: Cho phương trình bậc hai : ${x^2} – ( {2\sin \alpha – 1} )x + 6{\sin ^2}\alpha – \sin \alpha – 1 = 0$Trong đó $\alpha $ là tham sốa) Với những giá trị nào của $\alpha $ thì phương trình có nghiệm ?b) Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình trên. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức ${x^2}_1 + {x^2}_2$ khi $\alpha $ thay đổi.
Đề bài: Cho phương trình bậc hai : ${x^2} - ( {2\sin \alpha - 1} )x + 6{\sin ^2}\alpha - \sin \alpha - 1 = 0$Trong đó $\alpha $ là tham sốa) Với những giá trị nào của $\alpha $ thì phương trình có nghiệm ?b) Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình trên. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức ${x^2}_1 + {x^2}_2$ khi $\alpha $ thay đổi. Lời giải a) … [Đọc thêm...] vềĐề: Cho phương trình bậc hai : ${x^2} – ( {2\sin \alpha – 1} )x + 6{\sin ^2}\alpha – \sin \alpha – 1 = 0$Trong đó $\alpha $ là tham sốa) Với những giá trị nào của $\alpha $ thì phương trình có nghiệm ?b) Gọi ${x_1},{x_2}$ là hai nghiệm của phương trình trên. Tìm giá trị lớn nhất, nhỏ nhất của biểu thức ${x^2}_1 + {x^2}_2$ khi $\alpha $ thay đổi.
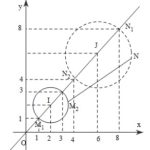
Đề: Cho $a,b,c,d$ là bốn số thực thỏa mãn các điều kiện: $\begin{cases}a^2+b^2+6=4(a+b) \\ c^2+d^2+64=12(c+d) \end{cases}$ Tìm GTLN, GTNN của biểu thức: $S=(a-c)^2+(b-d)^2$
Đề bài: Cho $a,b,c,d$ là bốn số thực thỏa mãn các điều kiện: $\begin{cases}a^2+b^2+6=4(a+b) \\ c^2+d^2+64=12(c+d) \end{cases}$ Tìm GTLN, GTNN của biểu thức: $S=(a-c)^2+(b-d)^2$ Lời giải Ta có: $\begin{cases}a^2+b^2+6=4(a+b) \\ c^2+d^2+64=12(c+d) \end{cases} \Leftrightarrow \begin{cases}(a-2)^2+(b-2)^2=2 \\ (c-6)^2+(d-6)^2=8 \end{cases}$ (I)Trong mặt phẳng tọa … [Đọc thêm...] vềĐề: Cho $a,b,c,d$ là bốn số thực thỏa mãn các điều kiện: $\begin{cases}a^2+b^2+6=4(a+b) \\ c^2+d^2+64=12(c+d) \end{cases}$ Tìm GTLN, GTNN của biểu thức: $S=(a-c)^2+(b-d)^2$
Đề: Tìm:a) GTNN :$f(x,y)=(x-y+1)^{2}+(3x+my+2)^{2} $b) GTLN,GTNN $C=2x+3y-2z $ với $\begin{cases}2x+y+3z=4 \\ 3x+4y-3z=6\\x,y,z\geq 0 \end{cases} $
Đề bài: Tìm:a) GTNN :$f(x,y)=(x-y+1)^{2}+(3x+my+2)^{2} $b) GTLN,GTNN $C=2x+3y-2z $ với $\begin{cases}2x+y+3z=4 \\ 3x+4y-3z=6\\x,y,z\geq 0 \end{cases} $ Lời giải Thêm lời giải chi tiết … [Đọc thêm...] vềĐề: Tìm:a) GTNN :$f(x,y)=(x-y+1)^{2}+(3x+my+2)^{2} $b) GTLN,GTNN $C=2x+3y-2z $ với $\begin{cases}2x+y+3z=4 \\ 3x+4y-3z=6\\x,y,z\geq 0 \end{cases} $
Đề: $\alpha ,\beta , \gamma $ là 3 góc dương thỏa mãn điều kiện $\alpha + \beta + \gamma = \frac{\pi }{2}$Tìm giá trị lớn nhất của biểu thức: $g = \sqrt {1 + \tan\alpha \tan\beta } + \sqrt {1 + \tan\beta \tan\gamma } + \sqrt {1 + \tan\gamma \tan\alpha } $
Đề bài: $\alpha ,\beta , \gamma $ là 3 góc dương thỏa mãn điều kiện $\alpha + \beta + \gamma = \frac{\pi }{2}$Tìm giá trị lớn nhất của biểu thức: $g = \sqrt {1 + \tan\alpha \tan\beta } + \sqrt {1 + \tan\beta \tan\gamma } + \sqrt {1 + \tan\gamma \tan\alpha } $ Lời giải Theo giả thiết ta có: $\pi /2 - \gamma = \alpha + \beta $$ \Rightarrow tg(\pi /2 - \gamma ) = … [Đọc thêm...] vềĐề: $\alpha ,\beta , \gamma $ là 3 góc dương thỏa mãn điều kiện $\alpha + \beta + \gamma = \frac{\pi }{2}$Tìm giá trị lớn nhất của biểu thức: $g = \sqrt {1 + \tan\alpha \tan\beta } + \sqrt {1 + \tan\beta \tan\gamma } + \sqrt {1 + \tan\gamma \tan\alpha } $
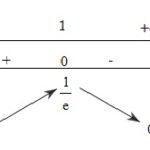
Đề: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm sốa) $f(x)=x^2 \ln x$ trên đoạn $[1;e].$b) $f(x)=x e^{-x}$ trên nửa khoảng $[0;\infty ).$
Đề bài: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm sốa) $f(x)=x^2 \ln x$ trên đoạn $[1;e].$b) $f(x)=x e^{-x}$ trên nửa khoảng $[0;\infty ).$ Lời giải a) Hàm số $f(x)=x^2 \ln x$ liên tục trên đoạn $[1;e]$ và có đạo hàm$f'(x)=2x \ln x+x^2 .\frac{1}{x}=x(2 \ln x+1), x\in [1;e]$$f'(x)=0\Leftrightarrow x=0\notin (1;e)$ hoặc $x=\frac{1}{\sqrt{e } }\notin [1;e]$và $f'(x) … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm sốa) $f(x)=x^2 \ln x$ trên đoạn $[1;e].$b) $f(x)=x e^{-x}$ trên nửa khoảng $[0;\infty ).$
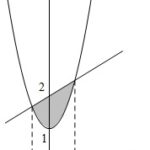
Đề: Cho parabol $y=x^2+1$ và đường thẳng $y = mx +2$.Hãy xác định $m$ để diện tích phẳng giới hạn bởi parabol và đường thẳng là nhỏ nhất.
Đề bài: Cho parabol $y=x^2+1$ và đường thẳng $y = mx +2$.Hãy xác định $m$ để diện tích phẳng giới hạn bởi parabol và đường thẳng là nhỏ nhất. Lời giải Phương trình hoành độ giao điểm của parabol và đường thẳng: $ x^2 + 1 = mx + 2 \Leftrightarrow x^2 - mx -1 =0 \Leftrightarrow \left[ \begin{array}{l}{x_1} = \frac{{m - \sqrt {{m^2} + 4} }}{2}\\{x_2} = \frac{{m + \sqrt … [Đọc thêm...] vềĐề: Cho parabol $y=x^2+1$ và đường thẳng $y = mx +2$.Hãy xác định $m$ để diện tích phẳng giới hạn bởi parabol và đường thẳng là nhỏ nhất.
Đề: Cho $a,b,c$ là ba số dương sao cho $abc=1$. Tìm giá trị nhỏ nhất của biểu thức :$Q=\frac{bc}{a^2(b+c)} + \frac{ca}{b^2(c+a)}+\frac{ab}{c^2(a+b)}$
Đề bài: Cho $a,b,c$ là ba số dương sao cho $abc=1$. Tìm giá trị nhỏ nhất của biểu thức :$Q=\frac{bc}{a^2(b+c)} + \frac{ca}{b^2(c+a)}+\frac{ab}{c^2(a+b)}$ Lời giải Đặt $\frac{1}{a}=x >0,\frac{1}{b}=y>0,\frac{1}{c}=z>0$.Ta có abc=$1 \Leftrightarrow xyz=1$Biểu thức Q trở thành $Q=\frac{x^2}{y+z}+\frac{y^2}{z+x}+\frac{z^2}{x+y} (2)$Áp dụng bất đẳng thức Svacxở vào $(2)$ … [Đọc thêm...] vềĐề: Cho $a,b,c$ là ba số dương sao cho $abc=1$. Tìm giá trị nhỏ nhất của biểu thức :$Q=\frac{bc}{a^2(b+c)} + \frac{ca}{b^2(c+a)}+\frac{ab}{c^2(a+b)}$
Đề: Cho $x,y,z>1$ thỏa $x+y+z=xyz$. Tìm giá trị nhỏ nhất của: $P=\frac{y-2}{x^2}+\frac{z-2}{y^2}+\frac{x-2}{z^2}$
Đề bài: Cho $x,y,z>1$ thỏa $x+y+z=xyz$. Tìm giá trị nhỏ nhất của: $P=\frac{y-2}{x^2}+\frac{z-2}{y^2}+\frac{x-2}{z^2}$ Lời giải Giải:Theo giả thiết: $\frac{1}{xy}+\frac{1}{yz}+\frac{1}{zx}=1$Ta có: $P=\frac{(x-1)+(y-1)}{x^2}+\frac{(y-1)+(z-1)}{y^2}+\frac{(z-1)+(x-z)}{z^2}-(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})$ … [Đọc thêm...] vềĐề: Cho $x,y,z>1$ thỏa $x+y+z=xyz$. Tìm giá trị nhỏ nhất của: $P=\frac{y-2}{x^2}+\frac{z-2}{y^2}+\frac{x-2}{z^2}$