Cực trị của hàm số

Đề: Cho hàm số: $y = \frac{x^2 + mx – 2m – 4}{x + 2}\,\,\,(1)$ ($m$ là tham số)$1.$ Tìm các điểm mà đồ thị hàm số ($1$) đi qua với mọi giá trị của $m.$$2.$ Xác định $m$ để hàm số ($1$) có cực đại và cực tiểu. Tìm quỹ tích của điểm cực đại của đồ thị khi $m$ thay đổi.$3.$ Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số ($1$) ứng với $m = -1$.

Ngày 10/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

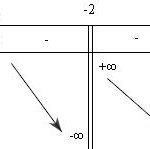
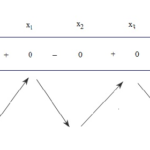
Đề bài: Cho hàm số: $y = \frac{x^2 + mx - 2m - 4}{x + 2}\,\,\,(1)$ ($m$ là tham số)$1.$ Tìm các điểm mà đồ thị hàm số ($1$) đi qua với mọi giá trị của $m.$$2.$ Xác định $m$ để hàm số ($1$) có cực đại và cực tiểu. Tìm quỹ tích của điểm cực đại của đồ thị khi $m$ thay đổi.$3.$ Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số ($1$) ứng với $m = -1$. Lời giải $1.$ ĐK: $x … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{x^2 + mx – 2m – 4}{x + 2}\,\,\,(1)$ ($m$ là tham số)$1.$ Tìm các điểm mà đồ thị hàm số ($1$) đi qua với mọi giá trị của $m.$$2.$ Xác định $m$ để hàm số ($1$) có cực đại và cực tiểu. Tìm quỹ tích của điểm cực đại của đồ thị khi $m$ thay đổi.$3.$ Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số ($1$) ứng với $m = -1$.

Đề: Cho hàm số $y = \frac{{3x – 1}}{{x – 3}}$$1.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2.$ Tìm giá trị lớn nhất, nhỏ nhất của hàm số đã cho khi $0 \le x \le 2$

Ngày 09/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

Đề bài: Cho hàm số $y = \frac{{3x - 1}}{{x - 3}}$$1.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2.$ Tìm giá trị lớn nhất, nhỏ nhất của hàm số đã cho khi $0 \le x \le 2$ Lời giải $1$. Bạn đọc tự giải.$2$. $y' = \frac{{ - 8}}{{{{\left( {x - 3} \right)}^2}}} \(\Rightarrow $ Hàm số nghịch biến trong đoạn $0 \le x \le 2$$\Rightarrow \mathop {\max y}\limits_{0 … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{3x – 1}}{{x – 3}}$$1.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2.$ Tìm giá trị lớn nhất, nhỏ nhất của hàm số đã cho khi $0 \le x \le 2$

Đề: Cho hàm số: $ y = mx^3 – 3mx^2 + (2m + 1)x + 3 – m (C_m) $ Tìm tất cả các giá trị của $m$ sao cho hàm số có cực đại, cực tiểu. Chứng minh rằng khi đó đường thẳng nối hai điểm cực đại, cực tiểu của $ (C_m) $ luôn đi qua một điểm cố định.

Ngày 09/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

Đề bài: Cho hàm số: $ y = mx^3 - 3mx^2 + (2m + 1)x + 3 - m (C_m) $ Tìm tất cả các giá trị của $m$ sao cho hàm số có cực đại, cực tiểu. Chứng minh rằng khi đó đường thẳng nối hai điểm cực đại, cực tiểu của $ (C_m) $ luôn đi qua một điểm cố định. Lời giải $ y' = 3m{x^2} - 6mx + 2m + 1 $ . Hàm số có cực đại, cực tiểu $ \Leftrightarrow y' $ có 2 nghiệm phân biệt $ … [Đọc thêm...] vềĐề: Cho hàm số: $ y = mx^3 – 3mx^2 + (2m + 1)x + 3 – m (C_m) $ Tìm tất cả các giá trị của $m$ sao cho hàm số có cực đại, cực tiểu. Chứng minh rằng khi đó đường thẳng nối hai điểm cực đại, cực tiểu của $ (C_m) $ luôn đi qua một điểm cố định.

Đề: Cho hàm số $y = – {x^4} + 2m{x^2}\left( {{C_m}} \right)$$1$. Khảo sát hàm số $\left( {{C_m}} \right)$ với $m = 1$$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm $A\left( {\sqrt 2 ,\,0} \right)$$3$. Hãy xác định m để hàm số $\left( {{C_m}} \right)$ có ba cực trị.

Ngày 09/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

Đề bài: Cho hàm số $y = - {x^4} + 2m{x^2}\left( {{C_m}} \right)$$1$. Khảo sát hàm số $\left( {{C_m}} \right)$ với $m = 1$$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm $A\left( {\sqrt 2 ,\,0} \right)$$3$. Hãy xác định m để hàm số $\left( {{C_m}} \right)$ có ba cực trị. Lời giải $1$. Bạn đọc tự giải.$2$. Với $m = 1$, có $y = f\left( … [Đọc thêm...] vềĐề: Cho hàm số \(y = – {x^4} + 2m{x^2}\left( {{C_m}} \right)$$1$. Khảo sát hàm số $\left( {{C_m}} \right)$ với $m = 1$$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm $A\left( {\sqrt 2 ,\,0} \right)$$3$. Hãy xác định m để hàm số $\left( {{C_m}} \right)$ có ba cực trị.

Đề: Cho họ đường cong $y = \frac{{ – {x^2} + mx – {m^2}}}{{x – m}}\left( {{C_m}} \right)$$1$. Khảo sát sự biến thiên vẽ đồ thị đường cong khi $m = 1$$2$. Tìm $m$ để đường cong $\left( {{C_m}} \right)$ có điểm cực đại và cực tiểu$3$. Tìm các điểm trên mặt phẳng tọa độ sao cho có đúng hai đường của họ $\left( {{C_m}} \right)$ đi qua.

Ngày 09/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

Đề bài: Cho họ đường cong $y = \frac{{ - {x^2} + mx - {m^2}}}{{x - m}}\left( {{C_m}} \right)$$1$. Khảo sát sự biến thiên vẽ đồ thị đường cong khi $m = 1$$2$. Tìm $m$ để đường cong $\left( {{C_m}} \right)$ có điểm cực đại và cực tiểu$3$. Tìm các điểm trên mặt phẳng tọa độ sao cho có đúng hai đường của họ $\left( {{C_m}} \right)$ đi qua. Lời giải $1$. Bạn đọc tự … [Đọc thêm...] vềĐề: Cho họ đường cong $y = \frac{{ – {x^2} + mx – {m^2}}}{{x – m}}\left( {{C_m}} \right)$$1$. Khảo sát sự biến thiên vẽ đồ thị đường cong khi $m = 1$$2$. Tìm $m$ để đường cong $\left( {{C_m}} \right)$ có điểm cực đại và cực tiểu$3$. Tìm các điểm trên mặt phẳng tọa độ sao cho có đúng hai đường của họ $\left( {{C_m}} \right)$ đi qua.

Đề: Biết $a < b < c$. Xem hàm số $y = (x - a)(x - b)(x - c)$1) Chứng tỏ rằng y có cực đại và cực tiểu.2) Xác định vị trí hoành độ của cực đại và cực tiểu đối với $a, b, c$.3) Giả sử $b = 0$. Tìm liên hệ giữa $a, c$ để điểm uốn của đồ thị nằm trên đường cong $y = {x^3}$

Ngày 08/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

Đề bài: Biết $a < b < c$. Xem hàm số $y = (x - a)(x - b)(x - c)$1) Chứng tỏ rằng y có cực đại và cực tiểu.2) Xác định vị trí hoành độ của cực đại và cực tiểu đối với $a, b, c$.3) Giả sử $b = 0$. Tìm liên hệ giữa $a, c$ để điểm uốn của đồ thị nằm trên đường cong $y = {x^3}$ Lời giải $1)$ Hàm số xác định với mọi $x$, ta có$y' = (x - a)(x - b) + (x - a)(x - c) + (x - b)(x - … [Đọc thêm...] vềĐề: Biết $a < b < c$. Xem hàm số $y = (x - a)(x - b)(x - c)$1) Chứng tỏ rằng y có cực đại và cực tiểu.2) Xác định vị trí hoành độ của cực đại và cực tiểu đối với $a, b, c$.3) Giả sử $b = 0$. Tìm liên hệ giữa $a, c$ để điểm uốn của đồ thị nằm trên đường cong $y = {x^3}$

Đề: Cho hàm số: $y = mx^3 – 3mx^2 + (2m + 1)x + 3 – m \,\,\,\,\,(C_m)$. Tìm tất cả các giá trị của m sao cho hàm số có cực đại, cực tiểu. Chứng minh rằng khi đó đường thẳng nối hai điểm cực đại, cực tiểu của $(C_m)$ luôn đi qua một điểm cố định.

Ngày 07/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

Đề bài: Cho hàm số: $y = mx^3 - 3mx^2 + (2m + 1)x + 3 - m \,\,\,\,\,(C_m)$. Tìm tất cả các giá trị của m sao cho hàm số có cực đại, cực tiểu. Chứng minh rằng khi đó đường thẳng nối hai điểm cực đại, cực tiểu của $(C_m)$ luôn đi qua một điểm cố định. Lời giải Ta có: $y' = 3m{x^2} - 6mx + 2m + 1$Hàm số có cực đại, cực tiểu $\Leftrightarrow y'=0$ có 2 nghiệm phân … [Đọc thêm...] vềĐề: Cho hàm số: $y = mx^3 – 3mx^2 + (2m + 1)x + 3 – m \,\,\,\,\,(C_m)$. Tìm tất cả các giá trị của m sao cho hàm số có cực đại, cực tiểu. Chứng minh rằng khi đó đường thẳng nối hai điểm cực đại, cực tiểu của $(C_m)$ luôn đi qua một điểm cố định.

Đề: Tìm tất cả các giá trị của tham số $m$ để đồ thị hàm số: $y = {x^2} – 3x + \frac{m}{x} + 3$ có $3$ điểm cực trị.Khi đó chứng minh rằng cả ba điểm cực trị này đều nằm trên đường cong : $y = 3(x-1)^2$

Ngày 06/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

Đề bài: Tìm tất cả các giá trị của tham số $m$ để đồ thị hàm số: $y = {x^2} - 3x + \frac{m}{x} + 3$ có $3$ điểm cực trị.Khi đó chứng minh rằng cả ba điểm cực trị này đều nằm trên đường cong : $y = 3(x-1)^2$ Lời giải Ta có $y^/=2x-3-\frac{m}{x^2} =\frac{2x^3-3x^2-m}{x^2} $Hàm số có ba điểm cực trị $\Leftrightarrow y^/$ có ba nghiệm phân biệt … [Đọc thêm...] vềĐề: Tìm tất cả các giá trị của tham số $m$ để đồ thị hàm số: $y = {x^2} – 3x + \frac{m}{x} + 3$ có $3$ điểm cực trị.Khi đó chứng minh rằng cả ba điểm cực trị này đều nằm trên đường cong : $y = 3(x-1)^2$

Đề: Cho hàm số $y = \frac{{{x^2} + 2{m^2}x + {m^2}}}{{x + 1}}$1) Với giá trị nào của $m$ thì hàm số có cực trị?2) Xác định $m$ để đồ thị của hàm số có 2 điểm đối xứng với nhau qua gốc tọa độ.3) Khảo sát sự biến thiên và vẽ đồ thị ứng với $m = 2$

Ngày 06/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

Đề bài: Cho hàm số $y = \frac{{{x^2} + 2{m^2}x + {m^2}}}{{x + 1}}$1) Với giá trị nào của $m$ thì hàm số có cực trị?2) Xác định $m$ để đồ thị của hàm số có 2 điểm đối xứng với nhau qua gốc tọa độ.3) Khảo sát sự biến thiên và vẽ đồ thị ứng với $m = 2$ Lời giải $1)$ Ta có $y = x + 2{m^2} - 1 + \frac{{1 - {m^2}}}{{x + 1}}$, do đó$y' = 1 - \frac{{1 - … [Đọc thêm...] vềĐề: Cho hàm số $y = \frac{{{x^2} + 2{m^2}x + {m^2}}}{{x + 1}}$1) Với giá trị nào của $m$ thì hàm số có cực trị?2) Xác định $m$ để đồ thị của hàm số có 2 điểm đối xứng với nhau qua gốc tọa độ.3) Khảo sát sự biến thiên và vẽ đồ thị ứng với $m = 2$

Đề: Cho hàm số: $y = \frac{{x^2 + (m + 1)x – m + 1}}{x – m}$$1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 2.$$2.$ Chứng minh rằng tích các khoảng cách từ một điểm tùy ý thuộc đồ thị hàm số (với $m = 2$ ở câu trên) tới hai đường tiệm cận luôn bằng một hằng số.$3.$ Với giá trị nào của $m$ thì hàm số đã cho có cực đại, cực tiểu đồng thời giá trị cực đại và giá trị cực tiểu cùng dấu.

Ngày 05/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

Đề bài: Cho hàm số: $y = \frac{{x^2 + (m + 1)x - m + 1}}{x - m}$$1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 2.$$2.$ Chứng minh rằng tích các khoảng cách từ một điểm tùy ý thuộc đồ thị hàm số (với $m = 2$ ở câu trên) tới hai đường tiệm cận luôn bằng một hằng số.$3.$ Với giá trị nào của $m$ thì hàm số đã cho có cực đại, cực tiểu đồng thời giá trị cực đại và giá … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{{x^2 + (m + 1)x – m + 1}}{x – m}$$1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 2.$$2.$ Chứng minh rằng tích các khoảng cách từ một điểm tùy ý thuộc đồ thị hàm số (với $m = 2$ ở câu trên) tới hai đường tiệm cận luôn bằng một hằng số.$3.$ Với giá trị nào của $m$ thì hàm số đã cho có cực đại, cực tiểu đồng thời giá trị cực đại và giá trị cực tiểu cùng dấu.