Đề bài: Cho hàm số $f(x) = \frac{4}{3}{x^3} - 2(1 - \sin a){x^2} + (1 + \cos2a)x + 1$. Tìm a để hàm số đạt cực trị tại $x_1,x_2 $ thảo mãn điều kiện: $x_1^2 + x_2^2 = 1$ Lời giải Hàm số có CĐ, CT \( \Leftrightarrow f'(x) = 4{x^2} - 4(1 - \sin a)x + (1 + c{\rm{os}}2a) = 0\) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' = 4{(1 - \sin a)^2} - 4(1 + \cos2a) > … [Đọc thêm...] vềĐề: Cho hàm số $f(x) = \frac{4}{3}{x^3} – 2(1 – \sin a){x^2} + (1 + \cos2a)x + 1$. Tìm a để hàm số đạt cực trị tại $x_1,x_2 $ thảo mãn điều kiện: $x_1^2 + x_2^2 = 1$
Cực trị của hàm số
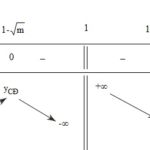
Đề: Xét hàm số $y = – 2x + k\sqrt {{x^2} + 1} $a) Với $k = 3$ hãy lập bảng biến thiên của hàm số và xác định các tiệm cận của đồ thị.b) Với giá trị nào của $k$ thì hàm số có cực tiểu.
Đề bài: Xét hàm số $y = - 2x + k\sqrt {{x^2} + 1} $a) Với $k = 3$ hãy lập bảng biến thiên của hàm số và xác định các tiệm cận của đồ thị.b) Với giá trị nào của $k$ thì hàm số có cực tiểu. Lời giải a) Với $k = 3$, ta có hàm số $y = - 2x + 3\sqrt {{x^2} + 1} $Hàm số được xác định với mọi $x$ và có đạo hàm $y' = - 2 + \frac{{3x}}{{\sqrt {{x^2} + 1} }} = … [Đọc thêm...] vềĐề: Xét hàm số $y = – 2x + k\sqrt {{x^2} + 1} $a) Với $k = 3$ hãy lập bảng biến thiên của hàm số và xác định các tiệm cận của đồ thị.b) Với giá trị nào của $k$ thì hàm số có cực tiểu.
Đề: Cho hàm số \(y = 2x – 1 + \frac{{2m}}{{x – 1}}\)$1$. Khảo sát và vẽ đồ thị của hàm số khi $m = 1$.$2$. Với giá trị nào của $m$ thì hàm số đồng thời có cực đại và cực tiểu.$3$. Tìm quỹ tích các điểm cực đại và cực tiểu của đồ thị hàm số khi $m$ thay đổi.
Đề bài: Cho hàm số \(y = 2x - 1 + \frac{{2m}}{{x - 1}}\)$1$. Khảo sát và vẽ đồ thị của hàm số khi $m = 1$.$2$. Với giá trị nào của $m$ thì hàm số đồng thời có cực đại và cực tiểu.$3$. Tìm quỹ tích các điểm cực đại và cực tiểu của đồ thị hàm số khi $m$ thay đổi. Lời giải $1$. Bạn đọc tự giải.$2$. Hàm số có cực đại và cực tiểu \( \Leftrightarrow y' = \frac{{2{x^2} - 4x + 2 … [Đọc thêm...] vềĐề: Cho hàm số \(y = 2x – 1 + \frac{{2m}}{{x – 1}}\)$1$. Khảo sát và vẽ đồ thị của hàm số khi $m = 1$.$2$. Với giá trị nào của $m$ thì hàm số đồng thời có cực đại và cực tiểu.$3$. Tìm quỹ tích các điểm cực đại và cực tiểu của đồ thị hàm số khi $m$ thay đổi.