Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Gọi \(S\) là tập hợp các giá trị nguyên của \(m\) sao cho phương trình \(\left( {m – 2} \right){.3^{2{x^2} + 2x + \frac{5}{2}}} – 2\left( {m + 1} \right){.3^{{x^2} + x + \frac{5}{4}}} + 2m – 6 = 0\) có nghiệm. Tổng các phần tử của \(S\) bằng A. 12. B. 18. C. 20. D. 14.

Ngày Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:,

Gọi \(S\) là tập hợp các giá trị nguyên của \(m\) sao cho phương trình \(\left( {m - 2} \right){.3^{2{x^2} + 2x + \frac{5}{2}}} - 2\left( {m + 1} \right){.3^{{x^2} + x + \frac{5}{4}}} + 2m - 6 = 0\) có nghiệm. Tổng các phần tử của \(S\) bằng A. 12. B. 18. C. 20. D. 14. Lời giải chi tiết PHÁT TRIỂN TƯƠNG TỰ CÂU 47 ĐỀ TOÁN THAM KHẢO 2021 CỦA BỘ. BIÊN SOẠN TỪ STRONG TEAM TOÁN … [Đọc thêm...] vềGọi \(S\) là tập hợp các giá trị nguyên của \(m\) sao cho phương trình \(\left( {m – 2} \right){.3^{2{x^2} + 2x + \frac{5}{2}}} – 2\left( {m + 1} \right){.3^{{x^2} + x + \frac{5}{4}}} + 2m – 6 = 0\) có nghiệm. Tổng các phần tử của \(S\) bằng A. 12. B. 18. C. 20. D. 14.

Ôn tập thi cuối kỳ 2 Toán 12 – TÍCH PHÂN

Ngày Thuộc chủ đề:Toán lớp 12 Tag với:

Ôn tập thi cuối kỳ 2 Toán 12 - NGUYÊN HÀM - TÍCH PHÂN - ỨNG DỤNG Cho hàm số $ f\left( x \right)=x\cdot \ln x$. Một nguyên hàm của hàm số $ g\left( x \right)=2x\cdot f'\left( x \right)$ là { $x^2\left( \ln x-\dfrac{1}{2} \right)$ } { $x^2\left( \ln x+\dfrac{1}{2} \right)$ } { $x^2\left( \ln x+1 \right)$ } { $x^2\left( \ln x-1 \right)$ } LỜI GIẢI Ta có $\displaystyle\int{2x\cdot … [Đọc thêm...] vềÔn tập thi cuối kỳ 2 Toán 12 – TÍCH PHÂN

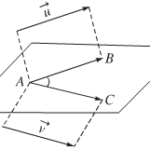
Bài 2: Hai đường thẳng vuông góc – Hình học 11

Ngày Thuộc chủ đề:Toán lớp 11 Tag với:

Học Toán 11 Chương 3 Bài 2: Hai đường thẳng vuông góc 1. Tóm tắt lý thuyết 1.1. Tích vô hướng của hai vectơ trong không gian a) Góc giữa hai vectơ trong không gian – Định nghĩa:  Trong không gian, cho \(\overrightarrow u \) và \(\overrightarrow v \) là hai vectơ khác vectơ – không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao … [Đọc thêm...] vềBài 2: Hai đường thẳng vuông góc – Hình học 11

Đề thi Toán 12 thử Lần 1 – Chuyên Hạ Long – 2021

Ngày Thuộc chủ đề:Đề thi toán Tag với:

Đề thi Toán 12 thử Lần 1 – Chuyên Hạ Long – 2021 - có lời giải chi tiết ======== 10 câu cuối === Câu 41. [Mức độ 3] Cho lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(a\). Trên các tia \(AA'\), \(BB'\)\(CC'\) lần lượt lấy các điểm \({A_1},{B_1},{C_1}\) cách mặt phẳng \(\left( {ABC} \right)\) các khoảng \(\frac{a}{2},\,\,a,\,\frac{{3a}}{2}\). Tính góc giữa hai mặt … [Đọc thêm...] vềĐề thi Toán 12 thử Lần 1 – Chuyên Hạ Long – 2021

ĐỀ ÔN HÌNH HỌC 12 THEO CHƯƠNG

Ngày Thuộc chủ đề:Đề thi HKI môn toán Tag với:

ĐỀ ÔN HÌNH HỌC 12 THEO CHƯƠNGBẢNG MÔ TẢ CHI TIẾT NỘI DUNG CÂU HỎICHỦ ĐỀ CÂU MỨC ĐỘ MÔ TẢChủ đề 1. Lý thuyết khối đa diện 1 NB Tìm số mặt của một hình đa diện.2 NB Phân chia khối đa diện. Chủ đề 2. Khối chóp có cạnh vuông góc với đáy 3 NB Tính thể tích khi biết chiều cao và dtích đáy của khối chóp (đáy hình vuông). 4 NB Tính thể tích khi biết chiều cao và dtích đáy của khối chóp … [Đọc thêm...] vềĐỀ ÔN HÌNH HỌC 12 THEO CHƯƠNG

Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA=a \sqrt{ 2} $  và vuông góc với đáya) Chứng minh rằng các mặt bên của hình chóp là các tam giác vuôngb) Gọi $(P)$ là mặt phẳng qua $A$ và vuông góc với $SC$. Dựng thiết diện của hình chóp $S.ABCD$ và mặt phẳng $(P)$. Tính diện tích thiết diện

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA=a \sqrt{ 2} $  và vuông góc với đáya) Chứng minh rằng các mặt bên của hình chóp là các tam giác vuôngb) Gọi $(P)$ là mặt phẳng qua $A$ và vuông góc với $SC$. Dựng thiết diện của hình chóp $S.ABCD$ và mặt phẳng $(P)$. Tính diện tích thiết diện Lời giải a) Ta có $SA \bot (ABCD)$ Suy ra $SA \bot … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA=a \sqrt{ 2} $  và vuông góc với đáya) Chứng minh rằng các mặt bên của hình chóp là các tam giác vuôngb) Gọi $(P)$ là mặt phẳng qua $A$ và vuông góc với $SC$. Dựng thiết diện của hình chóp $S.ABCD$ và mặt phẳng $(P)$. Tính diện tích thiết diện

Home

Đây là website về giải bài tập sách giáo khoa môn Toán từ lớp 1 đến lớp 12 của SGK Chân trời, Kết nối, Cánh diều, Xem và tải về sách giáo khoa môn Toán.Học Toán phổ thông online, Ôn thi TN THPT Quốc gia môn Toán và đề thi toán 2025. Bài viết mới MỖI NGÀY 1 ĐỀ TOÁN THI THỬ TN THPT 2025 Học Toán 12 Học Toán 11 Học Toán 10 SÁCH TOÁN TRẮC NGHIỆM TOÁN … [Đọc thêm...] vềHome

Học toán lớp 12

Ngày Thuộc chủ đề:Toán lớp 12 Tag với:,

Chương trình học Toán Lớp 12 GIẢI TÍCH LỚP 12 Chương 1: Ứng Dụng Đạo Hàm Để Khảo Sát Và Vẽ Đồ Thị Của Hàm Số ■ Bài 1 Sự đồng biến, nghịch biến của hàm số ■ Bài 2 Cực trị của hàm số ■ Bài 3 Giá trị lớn nhất và giá trị nhỏ nhất của hàm số ■ Bài 4 Đường tiệm cận ■ Bài 5 Khảo sát sự biến thiên và vẽ đồ thị của hàm số ■ Ôn tập chương I Ứng dụng đạo hàm để … [Đọc thêm...] vềHọc toán lớp 12

PHƯƠNG PHÁP GIẢI TOÁN CỰC TRỊ LOGARIT

Ngày Thuộc chủ đề:Sách toán 12 Tag với:

Tài Liệu – Đề Thi PHƯƠNG PHÁP GIẢI TOÁN CỰC TRỊ LOGARIT ======== Nội dung cuốn sách: Chương 1. Các kỹ thuật đánh giá cơ bản. I. Các kiến thức cơ bản. II. Các dạng toán cực trị mũ – logarit. 1. Kỹ thuật rút thế, đánh giá điều kiện đưa về hàm một biến số. 2. Kỹ thuật “hàm đặc trưng”. 3. Các bài toán liên quan tới định lý Viet. 4. Các bài toán đưa về đánh giá biến logb … [Đọc thêm...] vềPHƯƠNG PHÁP GIẢI TOÁN CỰC TRỊ LOGARIT

[Dạng câu 50 Toán L2 – 2020] Cho \(0\le x,y\le 1\) thỏa mãn\({{2020}^{1-x-y}}=\frac{{{x}^{2}}+2021}{{{y}^{2}}-2y+2022}.\) Gọi \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(S=2{{x}^{3}}+6{{y}^{3}}+3{{x}^{2}}-9xy\) Khi đó\(M+m\) bằng bao nhiêu?

Ngày Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:

Cho \(0\le x,y\le 1\) thỏa mãn\({{2020}^{1-x-y}}=\frac{{{x}^{2}}+2021}{{{y}^{2}}-2y+2022}.\) Gọi \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(S=2{{x}^{3}}+6{{y}^{3}}+3{{x}^{2}}-9xy\) Khi đó\(M+m\) bằng bao nhiêu? A. \(\frac{13}{2}\). B. \(\frac{11}{2}\). C. \(5\). D. \(\frac{25}{2}\). Lời giải Ta có … [Đọc thêm...] về[Dạng câu 50 Toán L2 – 2020] Cho \(0\le x,y\le 1\) thỏa mãn\({{2020}^{1-x-y}}=\frac{{{x}^{2}}+2021}{{{y}^{2}}-2y+2022}.\) Gọi \(M,m\) lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức \(S=2{{x}^{3}}+6{{y}^{3}}+3{{x}^{2}}-9xy\) Khi đó\(M+m\) bằng bao nhiêu?