DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 9. Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với mặt phẳng đáy, \(ABCD\) là hình chữ nhật có \(AD = 3a,\,AC = 5a\), góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng \(45^\circ \). Khi đó \(\cos \) của góc giữa đường … [Đọc thêm...] về9. Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với mặt phẳng đáy, \(ABCD\) là hình chữ nhật có \(AD = 3a,\,AC = 5a\), góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng \(45^\circ \). Khi đó \(\cos \) của góc giữa đường thẳng \(SD\) và mặt phẳng \(\left( {SBC} \right)\) bằng
Kết quả tìm kiếm cho: ty so
25. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(\widehat {BAC} = 60^\circ ,\)tam giác \(SAB\) vuông tại \(S\), \(SA = a,\,SB = a\sqrt 3 \). Măt phẳng \(\left( {SAB} \right)\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(M\) là trung điểm của \(SC\). Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BM\).
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 25. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(\widehat {BAC} = 60^\circ ,\)tam giác \(SAB\) vuông tại \(S\), \(SA = a,\,SB = a\sqrt 3 \). Măt phẳng \(\left( {SAB} \right)\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(M\) là … [Đọc thêm...] về25. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(\widehat {BAC} = 60^\circ ,\)tam giác \(SAB\) vuông tại \(S\), \(SA = a,\,SB = a\sqrt 3 \). Măt phẳng \(\left( {SAB} \right)\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(M\) là trung điểm của \(SC\). Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BM\).
21. Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\).
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 21. Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\). A. … [Đọc thêm...] về21. Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh bằng \(\sqrt 6 \). Biết rằng các mặt bên của hình chóp có diện tích bằng nhau và một trong các cạnh bên bằng \(3\sqrt 2 \). Tính thể tích nhỏ nhất của khối chóp \(S.ABC\).
15. Gọi \({S_0}\) là diện tích mặt cầu \(\left( S \right)\) ngoại tiếp hình chóp \(S.ABCD\) . Cho biết \(AB = 5\sqrt 2 ;BC = 6;CD = 2\sqrt 5 ;AD = 3\sqrt {10} ;d\left( {B,AC} \right) = d\left( {D,AC} \right)\) . Khi \({S_0}\) đạt giá trị nhỏ nhất thì giá trị lớn nhất của thể tích khối chóp \(S.ABCD\) bằng
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 15. Gọi \({S_0}\) là diện tích mặt cầu \(\left( S \right)\) ngoại tiếp hình chóp \(S.ABCD\) . Cho biết \(AB = 5\sqrt 2 ;BC = 6;CD = 2\sqrt 5 ;AD = 3\sqrt {10} ;d\left( {B,AC} \right) = d\left( {D,AC} \right)\) . Khi \({S_0}\) đạt giá trị nhỏ nhất thì giá … [Đọc thêm...] về15. Gọi \({S_0}\) là diện tích mặt cầu \(\left( S \right)\) ngoại tiếp hình chóp \(S.ABCD\) . Cho biết \(AB = 5\sqrt 2 ;BC = 6;CD = 2\sqrt 5 ;AD = 3\sqrt {10} ;d\left( {B,AC} \right) = d\left( {D,AC} \right)\) . Khi \({S_0}\) đạt giá trị nhỏ nhất thì giá trị lớn nhất của thể tích khối chóp \(S.ABCD\) bằng
10. Cho hình chóp \(S.ABCD\) có đáy là hình thang với \(AD{\rm{//}}BC\) và \(AD = 2BC\). Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của các cạnh \(SA\), \(BC\), \(CD\). Điểm \(Q\) thỏa mãn \(\overrightarrow {SQ} = 2\overrightarrow {QD} \). Gọi \(V\), \(V’\) lần lượt là thể tích của khối chóp \(S.ABCD\) và khối tứ diện \(MNPQ\). Khi đó \(\frac{{V’}}{V}\) bằng
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 10. Cho hình chóp \(S.ABCD\) có đáy là hình thang với \(AD{\rm{//}}BC\) và \(AD = 2BC\). Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của các cạnh \(SA\), \(BC\), \(CD\). Điểm \(Q\) thỏa mãn \(\overrightarrow {SQ} = 2\overrightarrow {QD} \). Gọi … [Đọc thêm...] về10. Cho hình chóp \(S.ABCD\) có đáy là hình thang với \(AD{\rm{//}}BC\) và \(AD = 2BC\). Gọi \(M\), \(N\), \(P\) lần lượt là trung điểm của các cạnh \(SA\), \(BC\), \(CD\). Điểm \(Q\) thỏa mãn \(\overrightarrow {SQ} = 2\overrightarrow {QD} \). Gọi \(V\), \(V’\) lần lượt là thể tích của khối chóp \(S.ABCD\) và khối tứ diện \(MNPQ\). Khi đó \(\frac{{V’}}{V}\) bằng
THỂ TÍCH TRONG PHÂN CHIA KHỐI ĐA DIỆN
THỂ TÍCH TRONG PHÂN CHIA KHỐI ĐA DIỆN Trong các bài toán thể tích khối đa diện diện , một số bài toán vận dụng hoặc vận dụng cao thườngđề cập đến việc phân chia đa diện , tính thể tích khối đa diện mới theo thể tích khối đa diện đã cho. Thầy cô cần tạo tình huống cho học trò có tư duy về việc so sánh thể tích các khối chóp , khối lăngtrụ từ những tư duy đơn giản như so … [Đọc thêm...] vềTHỂ TÍCH TRONG PHÂN CHIA KHỐI ĐA DIỆN
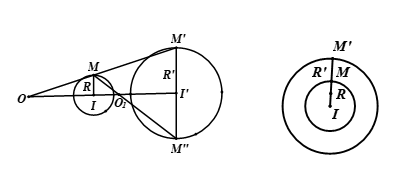
Bài 7: Phép vị tự – Chương 1 – Hình học 11
1. Định nghĩa Cho điểm \(I\) và một số thực \(k \ne 0\). Phép biến hình biến mỗi điểm \(M\) thành điểm \(M'\) sao cho \(\overrightarrow {IM'} = k.\overrightarrow {IM} \) được gọi là phép vị tự tâm \(I\) tỉ số \(k\). Kí hiệu \({V_{\left( {I;k} \right)}}\). 2. Tính chất - Nếu ${V_{\left( {I;k} \right)}}\left( M \right) = M',{V_{\left( {I;k} \right)}}\left( N \right) = … [Đọc thêm...] vềBài 7: Phép vị tự – Chương 1 – Hình học 11
Đề Kiểm Tra 1 tiết chương 1 Hình học 12 – Đề 2
Đề bài Câu 1: Cho khối chóp có thể tích \(V\), diện tích đáy là \(S\) và chiều cao \(h\). Chọn công thức đúng: A. \(V = Sh\) B. \(V = \dfrac{1}{2}Sh\) C. \(V = \dfrac{1}{3}Sh\) D. \(V = \dfrac{1}{6}Sh\) Câu 2: Một khối chóp có đáy là đa giác \(n\)cạnh. Trong các mệnh đề sau đây, mệnh đề nào đúng? A. Số mặt và số đỉnh bằng nhau B. … [Đọc thêm...] vềĐề Kiểm Tra 1 tiết chương 1 Hình học 12 – Đề 2
Đề: Tháp Eiffel ở Pháp cao 300 m, được làm hoàn toàn bằng sắt và nặng khoảng 8000000 kg. Người ta làm một mô hình thu nhỏ của tháp với cùng chất liệu và cân nặng khoảng 1 kg. Hỏi chiều cao của mô hình là bao nhiêu?
Câu hỏi: Tháp Eiffel ở Pháp cao 300 m, được làm hoàn toàn bằng sắt và nặng khoảng 8000000 kg. Người ta làm một mô hình thu nhỏ của tháp với cùng chất liệu và cân nặng khoảng 1 kg. Hỏi chiều cao của mô hình là bao nhiêu? A. 1,5 m B. 2 m C. 0,5 m D. 3 m Hãy chọn trả lời đúng trước khi xem đáp … [Đọc thêm...] vềĐề: Tháp Eiffel ở Pháp cao 300 m, được làm hoàn toàn bằng sắt và nặng khoảng 8000000 kg. Người ta làm một mô hình thu nhỏ của tháp với cùng chất liệu và cân nặng khoảng 1 kg. Hỏi chiều cao của mô hình là bao nhiêu?
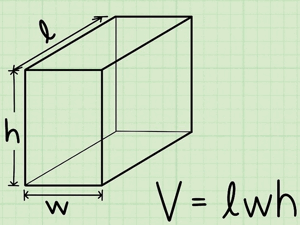
Bài 3 Khái niệm về thể tích của khối đa diện
Gồm các bài học sau (gồm có phần nâng cao và cơ bản): ============= Mời các bạn chọn phần cần đọc. =========== Lý thuyết thể tích của khối đa diện Công thức tính thể tích của 5 khối đa diện đều Công thức tính nhanh thể tích khối đa diện Các công thức tính nhanh Tỷ số thể tích khối đa diện Thể tích khối chóp Thể tích khối lăng trụ Tỷ số … [Đọc thêm...] vềBài 3 Khái niệm về thể tích của khối đa diện