1. Định nghĩa
Cho điểm \(I\) và một số thực \(k \ne 0\). Phép biến hình biến mỗi điểm \(M\) thành điểm \(M’\) sao cho \(\overrightarrow {IM’} = k.\overrightarrow {IM} \) được gọi là phép vị tự tâm \(I\) tỉ số \(k\).
Kí hiệu \({V_{\left( {I;k} \right)}}\).
2. Tính chất
– Nếu ${V_{\left( {I;k} \right)}}\left( M \right) = M’,{V_{\left( {I;k} \right)}}\left( N \right) = N’$ thì $\overrightarrow {M’N’} = k\overrightarrow {MN} $ và $M’N’ = \left| k \right|MN$
– Phép vị tự tỉ số \(k\) biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa ba điểm đó.
– Biến một đường thẳng thành một đường thẳng song song hoặc trùng với đường thẳng đã cho, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng.
– Biến một tam giác thành tam giác đồng dạng với tam giác đã cho, biến góc thành góc bằng nó.
– Biến đường tròn có bán kính \(R\) thành đường tròn có bán kính $\left| k \right|R$
3. Biểu thức tọa độ
Trong mặt phẳng tọa độ, cho $I\left( {{x_0};{y_0}} \right),M\left( {x;y} \right)$, gọi $M’\left( {x’;y’} \right) = {V_{\left( {I;k} \right)}}\left( M \right)$ thì $\left\{ \begin{array}{l}x’ = kx + \left( {1 – k} \right){x_0}\\y’ = ky + \left( {1 – k} \right){y_0}\end{array} \right.$.
4. Tâm vị tự của hai đường tròn
Định lí: Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia.
Tâm của phép vị tự này được gọi là tâm vị tự của hai đường tròn.
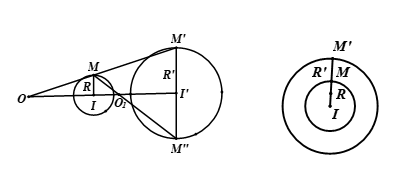
Cho hai đường tròn $\left( {I;R} \right)$ và $\left( {I’;R’} \right)$
– Nếu $I \equiv I’$ thì các phép vị tự ${V_{\left( {I; \pm \frac{{R’}}{R}} \right)}}$ biến $\left( {I;R} \right)$ thành $\left( {I’;R’} \right)$.
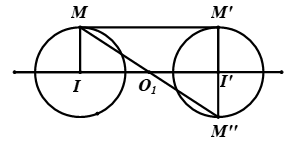
– Nếu $I \ne I’$ và $R \ne R’$ thì các phép vị tự ${V_{\left( {O;\frac{{R’}}{R}} \right)}}$ và ${V_{\left( {{O_1}; – \frac{{R’}}{R}} \right)}}$ biến $\left( {I;R} \right)$ thành $\left( {I’;R’} \right)$. Ta gọi $O$ là tâm vị tự ngoài còn ${O_1}$ là tâm vị tự trong của hai đường tròn.

Nếu $I \ne I’$ và $R = R’$ thì có ${V_{\left( {{O_1}; – 1} \right)}}$ biến $\left( {I;R} \right)$ thành $\left( {I’;R’} \right)$
Bài tập minh họa
Ví dụ 1:
Cho \(\Delta ABC\). Gọi E, F lần lượt là trung điểm của AB và AC. Tìm phép vị tự biến B và C tương ứng thành E và F.
Hướng dẫn giải:
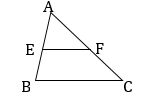
Vì BE và CF cắt nhau tại A nên A là tâm vị tự cần tìm.
Ta có:
\(\left\{ \begin{array}{l}{V_{\left( {A,k} \right)}}\left( B \right) = E \Leftrightarrow \overrightarrow {AE} = k\overrightarrow {AB} \\{V_{\left( {A,k} \right)}}\left( C \right) = F \Leftrightarrow \overrightarrow {AF} = k\overrightarrow {AC} \end{array} \right.\)
\(\left| k \right| = \frac{{\left| {\overrightarrow {AE} } \right|}}{{\left| {\overrightarrow {AB} } \right|}} = \frac{{\left| {\overrightarrow {AF} } \right|}}{{\left| {\overrightarrow {AC} } \right|}} = \frac{1}{2} \Rightarrow k = \frac{1}{2}\)
(do \(\overrightarrow {AE} \) và \(\overrightarrow {AB} \), \(\overrightarrow {AF} \) và \(\overrightarrow {AC} \) cùng hướng)
Vậy phép vị tự cần tìm là \({V_{\left( {A,\frac{1}{2}} \right)}}.\)
Ví dụ 2:
Cho \(\Delta ABC\) có A’, B’, C’ theo thứ tự là trung điểm của BC, CA, AB. Tìm một phép vị tự biến \(\Delta ABC\) thành \(\Delta A’B’C’\).
Hướng dẫn giải:
-Vì AA’, BB’, CC’ cắt nhau tại G nên G là tâm vị tự cần tìm.
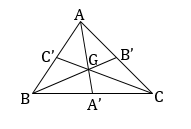
-Ta có: \({V_{\left( {G,k} \right)}}\left( A \right) = A’ \Leftrightarrow \overrightarrow {GA’} = k\overrightarrow {GA} \)
\(\left| k \right| = \frac{{\left| {\overrightarrow {GA’} } \right|}}{{\left| {\overrightarrow {GA} } \right|}} = \frac{1}{2} \Rightarrow k = – \frac{1}{2}\)
(do \(\overrightarrow {GA} \) và \(\overrightarrow {GA’} \) ngược hướng)
Vậy phép vị tự cần tìm là \({V_{\left( {G, – \frac{1}{2}} \right)}}.\)
Ví dụ 3:
Cho hai đường tròn \(\left( {O;2R} \right)\) và \(\left( {O’;R} \right)\) ngoài nhau. Tìm phép vị tự biến \(\left( {O;2R} \right)\) thành \(\left( {O’;R} \right)\).
Hướng dẫn giải:
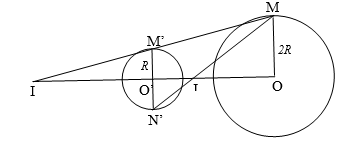
Lấy M bất kỳ trên \(\left( {O;2R} \right)\), vẽ đường thẳng qua O’ song song với OM cắt \(\left( {O’;R} \right)\) tại M’ và N’. Gọi MM’ cắt OO’ tại I, MN’ cắt OO’ tại J.
I là tâm vị tự ngoài, tỷ số vị tự \(k = \frac{R}{{2R}} = \frac{1}{2}\)
J là tâm vị tự trong, tỷ số vị tự \(k = – \frac{R}{{2R}} = – \frac{1}{2}\)
Ví dụ 4:
a) Cho \(A(1; – 3).\) Tìm tọa độ \(A’ = {V_{\left( {O; – 2} \right)}}(A).\)
b) Cho \(d:x + 2y + 3 = 0.\) Tìm phương trình \(d’ = {V_{\left( {I;2} \right)}}(d)\) biết I(1;2).
Hướng dẫn giải:
a) Gọi \({\rm{A’ (x’;y’)}}\)
Ta có \(A’ = {V_{\left( {O; – 2} \right)}}(A) \Rightarrow \overrightarrow {OA’} = – 2.\overrightarrow {OA} \Rightarrow (x’;y’) = – 2(1; – 3) \Rightarrow \left\{ \begin{array}{l}x’ = – 2\\y’ = 6\end{array} \right. \Rightarrow A'( – 2;6).\)
b) Chọn \(M( – 3;0) \in d.\)
Gọi \(M’ = {V_{(I;k)}}(M)\)
Ta có: \(\overrightarrow {IM} = \left( { – 4; – 2} \right)\)
\(M’ = {V_{(I;2)}}(M) \Rightarrow \overrightarrow {IM’} = 2\overrightarrow {IM} \Rightarrow \left\{ \begin{array}{l}{x_M}’ – 1 = – 8\\{y_M}’ – 2 = – 4\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_M}’ = – 7\\{y_M}’ = – 2\end{array} \right.\)
\( \Rightarrow M'( – 7; – 2) \in d’\)
Theo tính chất của phép vị tự d’ song song hoặc trùng với d suy ra đường thẳng d’ có một VTPT là: \(\overrightarrow n = \left( {1;2} \right).\)
Vậy phương trình d’ là: \(1(x + 7) + 2(y + 2) = 0 \Leftrightarrow x + 2y + 11 = 0.\)
Ví dụ 5:
Tìm ảnh của (C): \({(x – 3)^2} + {(y + 1)^2} = 5\) qua phép vị tự tâm I(1;2), tỉ số k=-2.
Hướng dẫn giải:
Đường tròn \((C):{(x – 3)^2} + {(y + 1)^2} = 5\) có tâm \(M(3; – 1),\) bán kính \(R = \sqrt 5 .\)
Gọi đường tròn (C’) có tâm M’(x’;y’), bán kính R’ là ảnh của của (C).
Do \(k = – 2 \Rightarrow R’ = 2\sqrt 5 .\)
Ta có: \(\overrightarrow {IM} = \left( {2; – 3} \right)\)
\({V_{\left( {I; – 2} \right)}}(M) = M’ \Rightarrow \overrightarrow {IM’} = – 2\overrightarrow {IM} \Rightarrow \left\{ \begin{array}{l}x’ – 1 = – 4\\y’ – 2 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x’ = – 3\\y’ = 8\end{array} \right. \Rightarrow M'( – 3;8).\)
Vậy phương trình đường tròn (C’) là: \({(x + 3)^2} + {(y – 8)^2} = 20.\)
