Bài 5: Phép quay – Chương 1 – Hình học 11

1. Định nghĩa

Cho điểm \(O\) và góc lượng giác \(\alpha \). Phép biến hình biến \(O\) thành chính nó và biến mỗi điểm \(M \ne O\) thành điểm \(M’\) sao cho \(OM’ = OM\) và góc lượng giác \(\widehat {\left( {OM,OM’} \right)} = \alpha \) được gọi là phép quay tâm \(O\), góc quay \(\alpha \).

Kí hiệu: \({Q_{\left( {O,\alpha } \right)}}\)

– Khi \(\alpha  = \left( {2k + 1} \right)\pi ,k \in Z\) thì \({Q_{\left( {O,\alpha } \right)}}\) là phép đối xứng tâm \(O\).

– Khi \(\alpha  = k2\pi \left( {k \in Z} \right)\) thì \({Q_{\left( {O,\alpha } \right)}}\) là phép đồng nhất.

2. Tính chất của phép quay

– Bảo toàn khoảng cách giữa hai điểm bất kì.

– Biến một đường thẳng thành đường thẳng.

– Biến một đoạn thẳng thành đoạn thẳng.

– Biến một tam giác bằng tam giác đã cho.

– Biến đường tròn thành đường tròn có cùng bán kính.

Giả sử phép quay tâm \(I\) góc quay \(\alpha \) biến đường thẳng \(d\) thành đường thẳng \(d’\), khi đó:

– Nếu \(0 < \alpha  \le \dfrac{\pi }{2}\) thì góc giữa hai đường thẳng \(d\) và \(d’\) bằng \(\alpha \).

– Nếu \(\dfrac{\pi }{2} < \alpha  < \pi \) thì góc giữa hai đường thẳng \(d\) và \(d’\) bằng \(\pi  – \alpha \).

3. Biểu thức tọa độ của phép quay

Trong mặt phẳng \(Oxy\), giả sử \(M\left( {x;y} \right)\) và \(M’\left( {x’;y’} \right) = {Q_{\left( {O,\alpha } \right)}}\left( M \right)\) thì \(\left\{ \begin{array}{l}x’ = x\cos \alpha  – y\sin \alpha \\y’ = x\sin \alpha  + y\cos \alpha \end{array} \right.\)

Trong mặt phẳng \(Oxy\), giả sử \(M\left( {x;y} \right),I\left( {a;b} \right)\) và \(M’\left( {x’;y’} \right) = {Q_{\left( {I,\alpha } \right)}}\left( M \right)\) thì \(\left\{ \begin{array}{l}x’ = a + \left( {x – a} \right)\cos \alpha  – \left( {y – b} \right)\sin \alpha \\y’ = b + \left( {x – a} \right)\sin \alpha  + \left( {y – b} \right)\cos \alpha \end{array} \right.\)

Bài tập minh họa

Ví dụ 1:

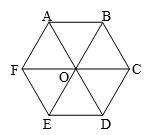
Cho lục giác đều ABCDEF tâm O. Hãy xác định ảnh của:

a) \(\Delta OAB\) qua phép quay tâm O, góc quay 360⁰.

b) \(\Delta OAB\) qua phép quay tâm O, góc quay 120⁰.

c) \(\Delta OAB\) qua phép quay tâm O, góc quay -180⁰.

d) \(\Delta OAB\) qua phép quay tâm O, góc quay -300⁰.

Hướng dẫn giải:

a) Ta có: \(\left\{ \begin{array}{l}{Q_{\left( {O{{,360}^0}} \right)}}\left( A \right) = A\\{Q_{\left( {O{{,360}^0}} \right)}}\left( B \right) = B\end{array} \right. \Rightarrow {Q_{\left( {O{{,360}^0}} \right)}}\left( {OAB} \right) = OAB\)

b) Ta có: \(\left\{ \begin{array}{l}{Q_{\left( {O{{,120}^0}} \right)}}\left( A \right) = E\\{Q_{\left( {O{{,120}^0}} \right)}}\left( B \right) = F\end{array} \right. \Rightarrow {Q_{\left( {O{{,120}^0}} \right)}}\left( {OAB} \right) = OEF.\)

c) Ta có: \(\left\{ \begin{array}{l}{Q_{\left( {O, – {{180}^0}} \right)}}\left( A \right) = D\\{Q_{\left( {O, – {{180}^0}} \right)}}\left( B \right) = E\end{array} \right. \Rightarrow {Q_{\left( {O, – {{180}^0}} \right)}}\left( {OAB} \right) = ODE.\)

d) Ta có: \(\left\{ \begin{array}{l}{Q_{\left( {O, – {{300}^0}} \right)}}\left( A \right) = F\\{Q_{\left( {O, – {{300}^0}} \right)}}\left( B \right) = A\end{array} \right. \Rightarrow {Q_{\left( {O, – {{300}^0}} \right)}}\left( {OAB} \right) = OFA.\)

 

Ví dụ 2:

Trong mặt phẳng Oxy cho điểm M(2;0) và đường thẳng d: \(x + 2y – 2 = 0,\) đường tròn \(\left( C \right):\) \({x^2} + {y^2} – 4x = 0.\) Xét phép quay Q tâm O góc quay \({90^0}.\)

a) Tìm ảnh của điểm M qua phép quay Q.

b) Tìm ảnh của d qua phép quay Q.

c) Tìm ảnh của (C) qua phép quay Q.

Hướng dẫn giải:

a) Ta có: Vì \(M(2;0) \in Ox\) nên: \({Q_{\left( {0;{{90}^0}} \right)}}(M) = M’:\left\{ \begin{array}{l}M’ \in Oy\\OM = OM’\end{array} \right. \Rightarrow M'(0;2).\)

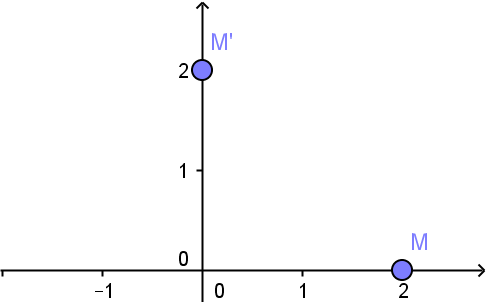
b) Ta có \(M\left( {2;0} \right) \in d,\) ảnh của M qua phép quay Q theo câu a là M’(0;2).

Gọi d’ là ảnh của d qua Q ta có d’ là đường thẳng qua M’ và vuông góc với d.

Đường thẳng d có VTPT là \(\overrightarrow n  = \left( {1;2} \right),\) suy ra d’ có VTPT là \(\overrightarrow {n’}  = \left( {2; – 1} \right)\)

Vậy phương trình của d’ là: \(2(x – 0) – 1(y – 2) = 0 \Leftrightarrow 2x – y + 2 = 0.\)

c) Đường tròn (C) có tâm M(2;0) và bán kính R=2.

Ảnh của M qua Q là M’(0;2).

Gọi (C) là ảnh của (C) qua Q, (C’) có tâm M’ và bán kính R=2.

Vậy phương trình của (C’) là: \({(x – 0)^2} + {(y – 2)^2} = 4.\)

 

Ví dụ 3:

Tìm ảnh của điểm A(3;4) qua phép quay tâm O góc quay \({90^0}.\)

Hướng dẫn giải:

Với phép quay tâm O góc 90 độ điểm A thành A’(x;y) có tọa độ thỏa mãn: \(\begin{array}{l}\left\{ \begin{array}{l}OA = OA’\\(OA;OA’) = {90^0}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{3^2} + {4^2} = {x^2} + {y^2}\\\overrightarrow {OA} .\overrightarrow {OA’}  = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x^2} + {y^2} = 25\\3x + 4y = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x =  – 4\\y = 3\end{array} \right.\\\left\{ \begin{array}{l}x = 4\\y =  – 3\end{array} \right.\end{array} \right.\end{array}\)

Do \(\alpha  = {90^0} > 0\) phép quay theo chiều dương suy ra: \(A'( – 4;3).\)